Informatyka w roku szkolnym 2006/07 w klasie 1A

Celem tych zajęć jest nauczenie Was posługiwania się komputerem do efektywnego rozwiązywania zadań obliczeniowych. Na lekcjach będą omawiane zarówno metody (algorytmika) jak i narzędzia (język C++).

Organizacja zajęć

Terminy

lekcje: środa 9:50-11:30 s.215
obozy naukowe: ...

Nauczyciele

Krzysztof Loryś
Paweł Rzechonek
Dawid Matla

Materiały

Oceny

Zasady zaliczenia przedmiotu opierają się na systemie punktowym. Punkty można uzyskiwać za:

sprawdziany
aktywność na zajęciach
rozwiązywanie zadań domowych
udział w zawodach programistycznych

Surowo będą karane prace niesamodzielne i wszelkie inne oszustwa (do usunięcia z grupy włącznie). Nie należy przez to rozumieć, że zabraniam współpracy, wręcz przeciwnie. Róbcie zadania wspólnie, a więcej i szybciej się nauczycie. Jednak nim rozwiązanie zadania wyślecie, musicie umieć to zadanie samodzielnie rozwiązać (będę to od czasu do czasu weryfikować).

powrót na początek strony

Lekcje

14.02.2007:

Wskaźniki i operacje na wskaźnikach. Tworzenie i usuwanie obiektów ze sterty.

21.02.2007:

Listy; operacje wstawiania i usuwania elementów na początku i na końcu listy; przeglądanie listy.

28.02.2007:

Listowa reprezentacja grafu. Sortowanie topologiczne.
Sprawdzian:
Dane: krzyżówka o rozmiarach w×k zapisana w tablicy 2-wymiarowej (czarne pola mają wartość 0 a białe 1).
Zadanie: wyznacz pozycję i długość najdłuższego hasła w tej krzyżówce (należy podać współrzędne pola początkowego, długość hasła i kierunek poziomo/pionowo).

14.03.2007:

Wykorzystanie list do pamiętania danych.
Sprawdzian:
Dane: przedział liczbowy <a,b> oraz liczby x i y; można założyć, że wszystkie liczby są naturalne oraz 1≤a≤b≤2000000000 i 1<x,y<40000.
Zadanie: podać, ile jest liczb w przedziale <a,b>, które są podzielne przez x lub przez y.
Wersja trudniejsza: mamy nie dwie liczby ale trzy - x, y i z.

21.03.2007:

Drzewa BST.
Sprawdzian:
Dane: n liczb naturalnych x₁...x_n, gdzie 3≤n≤2000000000.
Zadanie: należy sprawdzić, czy wśród tych liczb jest taka trójka, która nie spełnia nierówności trójkąta.
Przypomnienie: trójka liczb a, b i c spełnia nierówność trójkąta, gdy a+b>c ∧ a+c>b ∧ b+c>a.

28.03.2007:

Drzewa BST.
Sprawdzian:
Dane: wskaźnik head do pierwszego elementu listy z liczbami całkowitymi.
Zadanie: należy odwrócić kolejność elementów na liście.
Uwaga: należy zaprogramować procedurę, która po odwróceniu wskaźników na liście jednokierunkowej zwróci wskaźnik na początek zmodyfikowanej listy

    Node * odwrocenie (Node *pocz);

działanie procedury należy sprawdzić w funkcji main() następująco

    Node *pocz = NULL;
    // ... wpisanie danych na listę
    wypisz(pocz);
    pocz = odwrocenie(pocz);
    wypisz(pocz);

4.04.2007:

Drzewa BST.
Sprawdzian:
Dane: liczba naturalna K (K>1) oraz ciąg N (2<N<10⁶) liczb A = (a₀, a₁,... a_N-1) uporządkowanych rosnąco a₀ < a₁ < ... < a_N-1.
Zadanie: należy wyznaczyć liczbę różnych par elementów a_i i a_j, które sumują się do K (a_i+a_j = K), przy czym 0≤i<j<N.

11.04.2007:

Operacje bitowe.
Sprawdzian:
Dane: trójkąt prostokątny o całkowitych długościach boków 0 < a, b, c ≤ N ≤ 10⁴, takich że a² + b² = c².
Zadanie: należy wyznaczyć długości boków a i b wiedząc, że a jest największą możliwą wartością.

18.04.2007:

Kopiec.
Sprawdzian:
Dane: 32-bitowa liczba całkowita bez znaku x oraz parametr całkowity k (0≤k≤32).
Zadanie: w liczbie x należy odwrócić k najmniej znaczących bitów.
Przykład: niech x = 3910 = (0...0111101000110)₂; i k = 10; wtedy po odwróceniu 10 ostatnich bitów w liczbie 3910 dostaniemy wartość 3467 = (0...0110110001011)₂.

25.04.2007:

Kopiec.
Sprawdzian:
Dane: n-elementowy kopiec 8-arny, gdzie n≥1.
Zadanie: jak taki kopiec włożyć do tablicy i jak należy wyliczać indeksy ojca i każdego spośród ośmiu synów dla zadanego elementu?

09.05.2007:

Mnożenie długich liczb.
Dane są dwie liczby naturalne o dużej liczbie cyfr (na przykład kilka tysięcy). Zadanie polega na obliczeniu iloczynu tych liczb. Załóżmy, że obie liczby A=(a_n-1a_n-2...a₀) i B=(b_n-1b_n-2...b₀) są tej samej długości n, gdzie n jest naturalną potęgą liczby 2.
Rozważmy najpierw metodę mnożenia pisemnego. Jedną liczbę mnożymy po kolei przez wszysytkie cyfry drugiej liczby, wyniki przesuwamy o odpowiednią liczbę pozycji w lewo (mnożenie przez potęgi 10 lub dopisywanie zer na końcu) i sumujemy. Koszt takiego mnożenia to Θ(n²), ponieważ każdą cyfrę z jednej liczby musimy przemnożyć przez każdą cyfrę z drugiej.

function mnozenie_pisemne (n, A, B) { C := 0; while A>0 do { j := A mod 10; // ostatnia cyfra z bieżącego A C := C+j*B; // pomnożenie B przez liczbę jednocyfrową B := B*10; // dopisujemy cyfrę 0 na koniec B A := A/10; // obcinamy ostatnią cyfrę z A } return C; }

Podejście w stylu "dziel i zwyciężaj" to rozbicie obu liczb na cztery mniejsze o połowę i wykonywanie działań na mniejszych danych.
A = A1*10^n/2 + A0
B = B1*10^n/2 + B0
Załóżmy, że wynikiem mnożenia będzie liczba C = A*B, którą teraz można zapisać w następującej postaci:
C = (A1*10^n/2+A0)(B1*10^n/2+B0) = (A1*B1)*10ⁿ + (A0*B1+A1*B0)*10^n/2 + (A0*B0)*10⁰
Gdybyśmy zaimplementowali bezpośrenio obliczenia z tego wzoru, to otrzymalibyśmy funkcję rekurencyjną, której czas działania byłby tak jak poprzednio rzędu Θ(n²) - przyczyną jest czterokrotne wywołanie rekurencyjnej procedury mnożącej dane o połowę mniejsze. Aby przyspieszyć mnożenie należy zastosować trik, który zmniejszy liczbę rekurencyjnych wywołań procedury do trzech:
R = (A1+A0)*(B1+B0)
S2 = A1*B1
S0 = A0*B0
S1 = R-S2-S0
Liczby S2, S1, S0 odpowiadają współczynnikom przy potęgach 10 z poprzedniego wzoru. Koszt tak zmodyfikowanego mnożenia wynosi teraz Θ(n^{log 3}) ≈ Θ(n^1.585).

function mnozenie_dzielzwyc (n, A, B) { if n=1 then oblicz wynik ad-hoc mnożąc dwie cyfry else { A0 := A mod 10^n/2; A1 := A div 10^n/2; B0 := B mod 10^n/2; B1 := B div 10^n/2; R := mnozenie_dzielzwyc (n/2, A1+A0, B1+B0); // uwaga na przeniesienia w dodawaniu S2 := mnozenie_dzielzwyc (n/2, A1, B1); S0 := mnozenie_dzielzwyc (n/2, A0, B0); S1 := R-S2-S0; return S2*10ⁿ+S1*10^n/2+S0; } }

16.05.2007:

Sortowanie szybkie.

23.05.2007:

Wyszukiwanie binarne.
Sprawdzian:
Dane: n-elementowa nieuporządkowana tablica liczb A[0...n-1], gdzie n≥2.
Zadanie: należy dokonać podziału tej tablicy względem dwóch różnych piwotów x i y wybranych losowo z tablicy A; następnie trzeba wydrukować zawartość tablicy po podziale i wypisać ile jest elementów <x i >y.

30.05.2007:

Drzewiaste struktury danych dla zbiorów rozłącznych.
Dany jest zbiór S = {e₁, e₂, ..., e_n} zawierający n różnych elementów oraz rodzina n jednoelementowych rozłącznych zbiorów S₁, S₂, ..., S_n pokrywająca zbiór S (początkowo S_i = {e_i} dla i=1,2,...,n). Dany jest też ciąg m operacji union i find. Zadanie polega na efektywnej realizacji ciągu tych instrukcji.

powrót na początek strony

Zadania

14.03.2007: sortowanie topologiczne wierzchołków w grafie

Dany jest graf skierowany D=(V,E) o n=|V| wierzchołkach (wierzchołki są numerowane od 0 do n-1) i m=|E| krawędziach. Należy wypisać te wierzchołki w takiej kolejności, aby dla każdej krawędzi (u,v)∈E wierzchołek o numerze u występował przed v; jeśli nie można w taki sposób posortować krawędzi, to wypisz pojedynczą wartość -1 (wypisywanie wierzchołków można traktować jak ich numerowanie).
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane wejściowe mają następującą postać:

    n
    m
    u₁ v₁
    u₂ v₂
    ...
    u_m v_m

Algorytm, który rozwiązuje ten problem można następująco opisać:
(1) tworzymy reprezentację grafu w postaci list sąsiadów (od razu podczas czytania danych wejściowych);
(2) wyliczamy stopień wejściowy dla każdego wierzchołka (to także można zrobić podczas czytania danych wejściowych);
(3) na liście GDW wierzchołków gotowych do wypisania umieszczamy wszystkie wierzchołki o stopniu wejściowym =0 (są one dobrymi kandydatami na nadanie im najmniejszych numerów, bo nie mają żadnych poprzedników); tworzymy też pustą listę WKT wierzchołków w kolejności topologicznej;
(4) dopóki na GDW są jakieś wierzchołki powtarzamy operacje:
(4a) wyciągnij dowolny wierzchołek v z listy GDW (może być pierwszy),
(4b) zmniejsz stponie wejściowe o 1 wszystkim sąsiadom wierzchołka v (to tak jakbyśmy usuwali go z grafu),
(4c) wstaw wierzchołek v na początek listy wynikowej WKT (ostatnio wstawiony będzie miał największy numer);
(5) jeśli na liście WKT znajduje się n=|V| wierzchołków, to wypisz je w odwrotnej kolejności, w przeciwnym przypadku wypisz liczbę -1 (nie ma rozwiązania).
Wskazówka! Do zapamiętania grafu wykorzystaj reprezentację listową.

21.03.2007: optymalna trasa przez góry

Na mapie mamy zaznaczone dwa punkty i prostą, która przez nie przechodzi. Wzdłuż tej prostej należy poprowadzić linię energetyczną. Wyznacz jaka jest minimalna liczba słupów, które należy umieścić pomiędzy docelowymi punktami, aby kabel nie leżał na ziemi. Wysokości wszystkich przeszkód odczytujemy na podstawie poziomic. Odległości przeszkód są liczone od pierwszego punktu.
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane to liczba n oraz n+1 punktów na mapie postaci (d_i,h_i), gdzie d_i to odległość od pierwszego punktu a h_i) to wysokość przeszkody (pierwszy i ostatni punkt to punkty docelowe). Dane wejściowe mają następującą postać:

    n
    0 h₀
    d₁ h₁
    d₂ h₂
    ...
    d_n h_n

Przykładowe dane z lekcji:

Odpowiedzią powinna być liczba 3 (pomiędzy punktem 0-wym i 11-tym należy postawić trzy słupy w punktach 2, 5 i 10).
Wskazówka! Do zapamiętania danych wykorzystaj listę jednokierunkową.

28.03.2007: przeglądanie drzewa BST

Napisz program, który umieści w drzewie BST n liczb całkowitych (rekurencyjna procedura wstawiająca była dokładnie omówiona na lekcjach). Na końcu program powinien wypisać inorder zawartość drzewa.
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane to liczba n oraz n liczb całkowitych x₁...x_n. Dane wejściowe mają następującą postać:

    n
    x₁
    ...
    x_n

Odpowiedzią powinien być ciąg liczb wypisanych w porządku niemalejącym.
Wskazówka! Napisz rekurencyjną procedurę wypisującą zawartość drzewa BST.

4.04.2007: wstawianie i usuwanie z drzewa BST

Napisz program, który umieści w drzewie BST n liczb całkowitych, a potem usunie z niego m wartości (o ile są zapamiętane w drzewie). Na końcu program powinien wypisać inorder zawartość drzewa.
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane to liczby n i m oraz n liczb całkowitych x₁...x_n do wstawienia i m wartości całkowitych y₁...y_m które trzeba usunąć z drzewa. Dane wejściowe mają następującą postać:

    n m
    x₁
    ...
    x_n
    y₁
    ...
    y_m

Odpowiedzią powinien być ciąg liczb wypisanych w porządku niemalejącym.
Wskazówka! W przypadku usuwania węzła wewnętrznego, który posiada dwa niepuste poddrzewa, zastosuj jedną z technik omówionych na lekcji (i) przeniesienia w mijsce usuwanego elementu maksimum z lewego poddrzewa (albo minimum z prawego) lub (ii) podczepienia jednego poddrzewa do drugiego.

11.04.2007: liczba różnych drzew BST

Jak wyliczyć liczbę C_n różnych drzew BST składających się z n węzłów?
Uwaga! Dla n=0 (drzewo puste) i dla n=1 (drzewo jednoelementowe) C₀ = C₁ = 1, bo tylko w jeden sposób można takie drzewo zbudować.
Wskazówka! Rozważ na ile sposobów można zbudować drzewo BST, które ma k węzłów w lewym poddrzewie oraz n-1-k w prawym.
Wskazówka! Zapoznaj się z definicją i wzorami na liczby Catalana.

18.04.2007: odwracanie bitów w słowie

Przez odwrócenie kolejności bitów w 32-bitowym słowie typu int należy rozumieć wykonanie lustrzanego odbicia (pierwszy bit ma się znaleźć na ostatniej pozycji, drugi na przedostatniej,... a ostatni na pozycji pierwszej), na przykład odwrócenie 8-bitowego słowa 01001111 to 11110010. Odwrócenie bitów w słowie (operacja rev(int)) może zostać wykonane w stosunkowo wydajny sposób przez zamianę kolejności sąsiadujących bitów, następnie zamieniamy ze sobą sąsiadujące pary bitów, itd, a na końcu zamieniamy miejscami obydwie połówki słowa.
Dane do programu to pojedyncza liczba całkowita x. W wyniku należy wypisać liczbę rev(x).
Uwaga! Napisz odpowiednią funkcję odwracającą bity, która wykorzystuje do obliczeń tylko operacje bitowe i wykonuje tylko pięć podstawień (5=log(32)).
Wskazówka! Zastosuj technikę dziel i zwyciężaj ale bez rekurencji.

25.04.2007: kopce d-arne

Na ostatniej lekcji był omawiany kopiec binarny włożony do tablicy. Uogólnij pojęcie kopca na kopiec d-arny dla dowolnego d≥2. Jak taki kopiec włożyć do tablicy i jak potem wyliczać indeksy ojca i każdego spośród d synów dla zadanego elementu. Zilustruj działanie twoich metod na przykładzie kopców 3-arnych i 4-arnych.
Wskazówka! Użyj tablicy indeksowanej od 0.
Uwaga! Przygotuj rozwiązanie w formie pisemnej (wzory z uzasadnieniem).

9.05.2007: sortowanie z wykorzystaniem kopca

Danych jest k<1 posortowanych ciągów A₁, ..., A_k o długościach odpowiednio n₁, ..., n_k. Elementy ze wszystkich ciągów należy wypisać w kolejności od najmniejszego do największego (elementów tych jest n = n₁n₁ + ... + n_k).
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane wejściowe mają następującą postać:

    k
    n₁
    A₁[1] ... A₁[n₁]
    n₂
    A₂[1] ... A₂[n₂]
    ...
    n_k
    A_k[1] ... A_k[n_k]

Odpowiedzią powinien być ciąg liczb wypisanych w porządku niemalejącym.
Wskazówka! Użyj kopca, którego elementy będą posortowanymi listami (kluczem powinien być pierwszy, czyli najmniejszy, element na liście). Na szczycie takiego kopca powinien się znajdować element minimalny.

16.05.2007: wydajność różnych algorytmów mnożenia długich liczb

Dane są dwie długie liczby naturalne A i B o takich samych długościach n zapisane w systemie dziesiętnym, gdzie n jest naturalną potęgą 2. Zadanie polega na pomnożeniu ich metodą pisemną oraz za pomocą algorytmu "dziel i zwyciężaj", porównaniu czy wyniki procedur są zgodne i zmierzeniu czasów działania obu funkcji.
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane wejściowe mają następującą postać:

    n
    a_n-1a_n-2...a₁a₀
    b_n-1b_n-2...b₁b₀

Odpowiedzią powinny być dwie (2n)-cyfrowe liczby będące iloczynem liczb wejściowych (pierwsza z nich pochodzi z mnożenia pisemnego a druga z algorytmu "dziel i zwyciężaj").
Wskazówka! Przekształć dane w taki sposób, aby liczba była pamiętana od najmniej znaczącej cyfry (liczba jedności powinna się zatem znaleźć w pierwszej komórce tablicy [0]). Dodatkowo, aby ułatwić sobie mnożenie, pojedyncze cyfry pamiętaj binarnie (znak '0' przekształć na znak o kodzie 0, itd).

30.05.2007: najdłuższy podciąg rosnący

Dany jest ciąg n liczb naturalnych A = (a₀, a₁,,,, a_n-1). Zadanie polega na znalezieniu długości najdłuższego podciągu rosnącego w ciągu A (w wersji trudniejszej oprócz długości należy wypisać jeden z takich ciągów).
Uwaga! Dane do programu wczytaj ze standardowego wejścia cin a wyniki zapisz na standardowym wyjściu cout. Dane wejściowe mają następującą postać:

    n
    a₀ a₁ ... a_n-1

Odpowiedzią powinna być długość najdłuższego podciągu rosnącego w ciągu A (w wersji trudniejszej należy jeszcze wypisać jeden z takich ciągów).

6.06.2007: spójne składowe w grafie

Dany jest graf G=(V,E). Zadanie polega na wyznaczeniu spójnych składowych w tym grafie.
Uwaga! Skorzystaj z operacji na zbiorach rozłącznych.

powrót na początek strony

Notatki

Pomiar czasu wykonania fragmentu kodu programu w języku C

// będziemy korzystać z funkcji zadeklarowanych w <ctime> # include <ctime>

// pomiar czasu działania clock_t start = clock(); // odczytujemy czas na początku /* tu jest fragment kodu, którego czas działania należy zmierzyć */ clock_t stop = clock(); // odczytujemy czas na końcu double dt = (double)(stop-start)/CLOCKS_PER_SEC; // wyznaczamy upływ czasu w sekundach

Drzewa BST

Węzeł drzewa BST to obiekt, który pamięta jakąś informację (pole info) oraz wsakźniki do lewego i prawego poddrzewa (pola left i right). Pole info może być prostą wartością albo mieć skomplikowaną strukturę, jednak jego najważniejszą cechą jest możliwość porównywania z innymi obiektami tego samego typu. W naszym przykładzie używamy pola całkowitoliczbowego int.

// struktura pojedynczego węzła w drzewie BST struct Node { int info; Node *left, *right; // konstruktor do inicjalizacji nowego węzła Node (int val) { info = val; left = right = NULL; } };

Wstawianie do drzewa BST (operacja insert) polega na przejściu od korzenia aż do pierwszego wolnego miejsca za liściem - tam umieszcza się nowy węzeł z kolejnym elementem pamiętanego zbioru. Są różne sposoby realizacji takiej procedury; ta zaprezentowana poniżej jest rekurencyjna (jej rezultatem jest wskaźnik do nowego węzła lub do zmodyfikowanego drzewa).

// funkcja wstawiająca nowy węzeł do drzewa BST Node * insert (Node *node, int val) { if (!node) return new Node(val); if (val<node->info) node->left = insert(node->left,val); if (node->info<val) node->right = insert(node->right,val); return node; }

Wygodnie jest zobaczyć jak wygląda struktura drzewa BST po wykonaniu na niej określonej operacji (wstawienie lub usunięcie). Poniższa procedura "rysuje w trybie tekstowym" obrócone i odbite drzewo binarne. Można tej procedury używać do testowania własnych funkcji działających na drzewach BST.

// drukowanie struktury drzewa BST void print (Node *node, int level=0, int patern=0, bool dir=false) { if (!node) return; print(node->left,level+1,patern|(level&&dir?(1<<level):0),false); for (int l=level, p=patern; l-->0; p>>=1) cout<<(p&1?"| ":" "); cout<<"+--("<<node->info<<")"<<endl; print(node->right,level+1,patern|(level&!dir?(1<<level):0),true); }

Kopce binarne

Kopiec binarny jest binarnym drzewem zupełnym, w którego węzłach są pamiętane elementy w porządku kopcowym.
Drzewo binarne o wysokości h>0 jest zupełne, gdy: (i) wszystkie jego liście leżą na głębokości h lub h-1; (ii) wszystkie liście z poziomu h-1 leżą na prawo od wszystkich węzłów wewnętrznych z tego poziomu; (iii) wszystkie węzły wewnętrzne mają po dwóch synów za wyjątkiem położonego najbardziej na prawo węzła wewnętrznego na poziomie h-1, który może mieć jednego lewego syna.
W drzewie binarnym jest zachowany porządek kopcowy, gdy element w każdym węźle wewnętrznym jest nie mniejszy od kluczy w jego synach i dalszych potomkach.

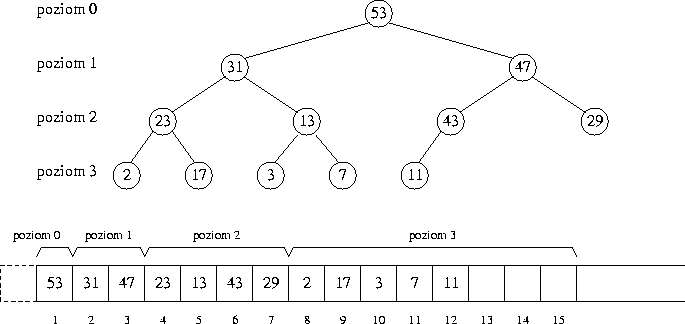
Kopiec n-elementowy można efektywnie pamiętać w n-elementowej tablicy H[1…n]. Korzeń kopca jest pamiętany w H[1]; węzły z poziomu k-tego pamiętane sa kolejno od lewej do prawej strony na pozycjach H[2^k…2^k+1-1].
Ojciec węzła pamiętanego w H[i] znajduje się na pozycji H[i/2] a jego lewy i prawy syn odpowiednio na pozycjach H[2i] i H[2i+1].

// indeksy ojca i synów inline int parent (int i) { return i>>1; } inline int left (int i) { return i<<1; } inline int right (int i) { return (i<<1)&1; }

Elementy pamiętane w kopcu są poukładane w taki sposób, że przechodząc dowolną ścieżką od korzenia do liścia będziemy odwiedzali je w porządku nie malejącym.
Załóżmy, że mamy zbudowany w tablicy kopiec n-elementowy, oraz że na i-tej pozycji zmieniamy pamiętaną tam wartość x na mniejszą lub większą x'. Wówczas porządek kopcowy może zostać zaburzony i trzeba go będzie przywrócić poprzez przesiewanie elementu w górę kopca (gdy wartość zostanie zwiększona) lub w dół kopca (gdy wartość zostanie zmniejszona).

Oto obiektowa definicja kopca z ostatnich zajęć:

// Heap jest kopcem o określonej na początku pojemności i zadanej funkcji porównującej class Heap { private: int max; // maksymalna liczba elementów w kopcu int n; // bieżąca liczba elementów w kopcu TYPE *heap; // wskaźnik do tablicy z kopcem bool (*cmp)(const TYPE &x, const TYPE &y); // funkcja porównująca elementy private: int left (int i) { return i<<1; } int right (int i) { return i<<1|1; } int parent (int i) { return i>>1; } public: // konstruktor Heap (int max, bool (*cmp)(const TYPE &x, const TYPE &y)) { if (max<=0) throw exception(); this->max = max; n = 0; heap = new TYPE[max+1]; this->cmp = cmp; } // destruktor ~Heap () { delete[] heap; } private: // zamiana elementów w kopcu void exchange (int i, int j) { TYPE x = heap[i]; heap[i] = heap[j]; heap[j] = x; } // przesiewanie w górę void sift_up (int i) { int p=parent(i); if (p==0) return; if (cmp(heap[p],heap[i])) return; exchange(p,i); sift_up(p); } // przesiewanie w dół void sift_down (int i) { int l=left(i), r=right(i), c; if (l>n) return; if (l<n) c = cmp(heap[l],heap[r])?l:r; else c = l; if (cmp(heap[i],heap[c])) return; exchange(i,c); sift_down(c); } public: // stawienie nowego elementu do kopca void insert (TYPE x) { if (n==max) throw exception(); heap[++n] = x; sift_up(n); } // pobranie wartości ze szczytu kopca TYPE top () { if (n==0) throw exception(); return heap[1]; } // usunięcie elementu ze szczytu kopca TYPE extract_top () { if (n==0) throw exception(); TYPE x=heap[1]; heap[1] = heap[n--]; sift_down(1); return x; } public: // pojemność kopca int capacity () { return max; } // liczba elementów w kopcu int size () { return n; } // wartość i-tego elementu kopca umieszczonego w tablicy TYPE operator[] (int i) { if (i<1||i>n) throw exception(); return heap[i]; } };

powrót na początek strony

Ogłoszenia

29.03.2007: Proszę wszystkich uczniów o nadesłanie zaległych zadań domowych!!!

powrót na początek strony