Informatyka w roku szkolnym 2008/09 w semestrze zimowym w klasie matematycznej 1A

Celem tych zajęć jest nauczenie Was wykorzystania komputera do efektywnego rozwiązywania zadań obliczeniowych. Na lekcjach będą omawiane zarówno metody rozwiązywania zadań (algorytmika) jak i narzędzia (maszyna RAM, język C).

Informacje organizacyjne

termin: środa 7:30-9:00 s.215
nauczyciel: Paweł Rzechonek

Ogłoszenia:

10.12.2008: Pilne!!! W styczniu 2009 r. będzie zorganizowany obóz informatyczny dla licealictów. Proszę się zapisywać jak najszybciej, najlepiej do końca tygodnia (później może nie być miejsc). Aby zapisać się na obóz należy wypełnić formularz zgłoszeniowy.
30.11.2008: Cały czas czekam na prawidłowe rozwiązanie zadania 9 z Czesiem biegającym po schodach. Za pierwsze prawidłowe rozwiązanie przyznam dodatkowo 5 punktów!!!
12.11.2008: Przypominam, że uczestnictwo w obozach, sparingach czy olimpiadach informatycznych jest nagradzane dodatkowymi punktami!
12.11.2008: Sobotni sparing zaczyna się o 9:00 w sali Wielkiej Wschodniej (s.25 na parterze, blisko portierni) w Instytucie Informatyki U.Wr. Zadania na sparingu będą zróżnicowane co do poziomu trudności, tak więc każdy będzie mógł znaleźć coś dla siebie ;-)
10.11.2008: W sobotę 15 listopada 2008 organizujemy sparing z programowania dla maszyny RAM w Instytucie Informatyki U.Wr. Obecność obowiązkowa!!! Zwolniony jest tylko Wojtek P.
28.10.2008: Udostępniłem Wam kompilator i interpreter dla maszyny RAM napisany przeze mnie w javie. Wypróbujcie jak działa :)
22.10.2008: Wszystkie osoby, które chciałyby pojechać na obóz informatyczny (trening przed olimpiadą) proszę o kontakt z profesorem Dawidem Matlą. Zachęcam do udziału!
17.10.2008: Uwaga, uzupełniłem treść zadania domowego o dodatkowy punkt: uzasadnienie poprawności algorytmu Agaty.
17.10.2008: Bardzo proszę, aby każdy uczeń wysłał maila do Rafała Rowaka. Potrzebuje on wasze adresy mailowe, żeby informować Was o Olimpiadzie i różnych innych zawodach informatycznych. W tytule listu proszę wpisać "jestem uczniem klasy 1A w XIV LO" a w teści podpisać się imieniem i nazwiskiem.
15.09.2008: W tym miejscu będą umieszczane różne informacje dotyczące organizacji zajęć. Proszę je czytać na bieżąco.

Pomoce dydaktyczne:

Maszyna RAM (Łukasz Szkup) działa tylko pod Windows na platformie .NET - błędy w implementacji dzielenia
Maszyna RAM (Wojciech Muła) działa w przeglądarce WWW - adersowanie pośrednie obsługuje się przez znak ∗ zamiast ˆ
Maszyna RAM (Paweł Rzechonek) uruchamiany z wiersza poleceń za pośrednictwem JVM (wirtualnej maszyny javy) - można go uruchamiać pod Windowsem i pod Linuksem

wstęp do programowania - notatki K.Lorysia uzupełnione przez R.Nowaka (IntroC.doc)
C++ Reference
C Standard Library
Marshall Brain: How C Programming Works
Steven Holmes: C Programming
C/C++ Directory in The Object Oriented Programming Web

Maszyna RAM

Udostępniam Wam w tym miejscu kompilator i interpreter dla maszyny RAM. Oba te programy zostały napisane w javie i po skompilowaniu umieszczone w jednym pliku ram.jar. Zarówno kompilator jak i interpreter uruchamia się z wiersza poleceń. Aby móc skorzystać z tych programów należy najpierw ściągnąć i zapisać lokalnie na komputerze plik ram.jar.

Programy źródłowe powinny mieć rozszerzenie .ram. W programach tych można posługiwać się nazwami symbolicznymi komórek pamięci - wystarczy na początku zadeklarować je instrukcją mem (zobacz do przykładów). Jeśli program jest poprawnie napisany, to po skompilowaniu dostaniemy plik z rozszerzeniem .ramcode, który nadaje się do uruchomienia w interpreterze.

Załóżmy, że plik ram.jar umieściliśmy w katalogu ścieżka/. Napisaliśmy też program dla maszyny RAM w pliku prog.ram. Aby go skompilować należy uruchomić w środowisku javy program ramc pisząc w wierszu poleceń:
user@computer:~> java -cp ścieżka/ram.jar ramc prog
Kompilator wypisuje na standardowe wyjście dla błędów sporo różnych komunikatów. Jeśli program zawiera błędy, to dostaniemy informację co to za błąd i w której linii się znajduje. Jeśli program się skompiluje to dostaniemy komunikat o sukcesie i plik wynikowy prog.ramcode. Aby wykonać skompilowany program należy uruchomić w środowisku javy program ram pisząc w wierszu poleceń:
user@computer:~> java -cp ścieżka/ram.jar ram prog
Czytanie danych z taśmy wejściowej w programie (rozkaz read) jest zastąpione przez czytanie z klawiatury, a pisanie na taśmę wyjściową (rozkaz write) przez pisanie na ekran.

Program będzie rozpowszechniany na licencji GNU GPL (Powszechna Licencja Publiczna GNU). Z warunkami licencji można się zapoznać na stronach Free Software Fundation.

powrót na początek strony

Zasady oceniania

Zasady zaliczenia przedmiotu opierają się na systemie punktowym. Punkty można uzyskiwać za:

sprawdziany
aktywność na zajęciach
rozwiązywanie zadań domowych
udział w zawodach programistycznych

Surowo będą karane prace niesamodzielne i wszelkie inne oszustwa (do usunięcia z grupy włącznie). Nie należy przez to rozumieć, że zabraniam współpracy, wręcz przeciwnie. Róbcie zadania wspólnie, a więcej i szybciej się nauczycie. Jednak nim rozwiązanie zadania wyślecie, musicie umieć to zadanie samodzielnie rozwiązać (będzie to weryfikowane).

powrót na początek strony

Notatki z lekcji

Spis treści:

agitacja, liczby Fibonacciego
schematy blokowe, szybkie potęgowanie, budowa maszyny RAM
skoki w programach na maszynę RAM, przetwarzanie ciągów liczbowych
operacja modulo, algorytm Euklidesa
binarna reprezentacja liczb w komputerach
przetwarzanie tablic na maszynie RAM
wprowadzenie do języka C++: we/wy, zmienne, wyrażenia, instrukcje
wprowadzenie do języka C++: instrukcje, tablice
wprowadzenie do języka C++: funkcje i rekurencja
wprowadzenie do języka C++: typy danych
wprowadzenie do języka C++: wskaźniki

10.09.2008: agitacja

Zadanie

Czesio ma do pokonania n>0 schodów. Czesio jest jeszcze mały i ma krótkie nogi, więc może pokonywać schody przechodząc dalej o 1 albo 2 stopnie. Chciałby też codziennie przechodzić je inaczej. Pomóż Czesiowi obliczyć, przez ile dni będzie je mógł pokonywać codziennie w inny sposób.

Rozwiązanie

W przypadku małych danych można sobie policzyć na palcach na ile sposobów można wejść po schodach pokonując je co jeden bądź co dwa stopnie. Przejście n schodów można zapisać jako ciąg złożony z liczb 1 i 2, którego suma wszystkich wyrazów jest równa n. Rozważmy kilka początkowych przypadków.

Dla n = 1 mamy 1 ciąg: (1).
Dla n = 2 mamy 2 ciągi: (1,1), (2).
Dla n = 3 mamy 3 ciągi: (1,1,1), (2,1), (1,2).
Dla n = 4 mamy 5 ciągów: (1,1,1,1), (2,1,1), (1,2,1), (1,1,2), (2,2).

Jak to uogólnić? Załóżmy, że ilość różnych ciągów złożonych z liczb 1 i 2, których wyrazy sumują się do n jest określona pewną funkcją g(n). Rozważmy pierwszy krok wykonany przez Czesia - może on przejść jeden stopień albo dwa stopnie naraz. Gdy pierwszy krok Czesia będzie mały i przejdzie on jeden stopień, to resztę stopni będzie mógł pokonać na g(n-1) sposobów; gdy jego pierwszy krok będzie duży i przeskoczy on dwa stopnie, to resztę stopni będzie mógł pokonać na g(n-2) sposobów. W sumie liczba różnych sposobów na pokonanie n schodów wynosi g(n) = g(n-1) + g(n-2). Można łatwo zauważyć, że g(n) = F(n+1), gdzie F_n to ciąg Fibonacciego.

Liczby Fibonacciego

Ciąg Fibonacciego F_n definiujemy następująco:
F₀ = 0
F₁ = 1
F_n = F_n-1+F_n-2 dla n≥2

Obliczanie liczb Fibonacciego

Metoda iteracyjna

Metoda iteracyjna polega na wyliczeniu kolejno wszystkich wyrazów ciągu Fibonacciego aż do n-tego włącznie. W obliczeniach korzystamy z wzoru rekurencyjnego. W trakcie obliczeń wystarczy pamiętać tylko trzy wyrazy tego ciągu. Oto schemat blokowy przedstawiający metodę iteracyjną:

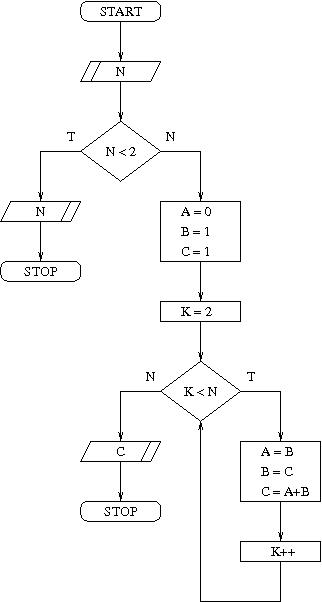
Metoda macierzowa

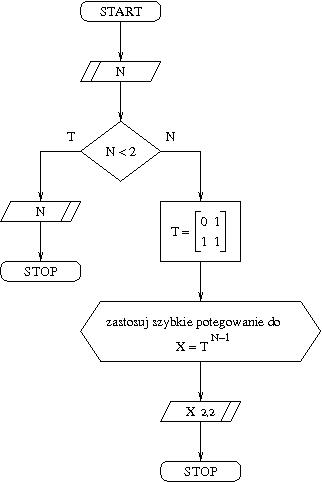
Metoda macierzowa używa macierzy transformacji

0	1
1	1

do wyliczenia kolejnych wyrazów ciągu Fibonacciego. W metodzie tej korzystamy z faktu, że mnożenie macierzy jest operacją łączną. Stosując w obliczeniach procedurę szybkiego potęgowania, koszt obliczenia n-tej liczby Fibonacciego jest logarytmiczny względem n. Oto schemat blokowy przedstawiający metodę macierzową:

17.09.2008: schematy blokowe, szybkie potęgowanie, budowa maszyny RAM

Schematy blokowe

Kilka użytecznych linków:

Szybkie potęgowanie

Mamy dane dwie liczby: x oraz n, przy czym n jest liczbą naturalną. Zadanie polega na efektywnym wyliczeniu potęgi xⁿ.

Metoda naiwna polega na wymnożeniu (n-1)-krotnie wartości x przez siebie, czyli xⁿ = x·x·...·x. Algorytm ten wykona więc n-1 mnożeń. Gdy n jest małe, to algorytm naiwny jest akceptowalny. Dla większych wartości n można skorzystać z metody szybkiego potęgowania.

Zauważmy, że jeśli wykładnik n jest potęgą 2, to xⁿ można szybko obliczyć podnosząc do kwadratu kolejno otrzymywane wartości:

x² = x·x
x⁴ = (x²)² = x²·x²
x⁸ = (x⁴)² = x⁴·x⁴
itd

Liczba wykonywanych w takim przypadku obliczeń jest logarytmiczna względem wartości n. Jeśli chcielibyśmy obliczyć x^1048576, to postępując w ten sposób wystarczy wykonać tylko 20 mnożeń, ponieważ 1048576=2²⁰. Algorytm naiwny wykonałby ich aż 1048575!

Algorytm szybkiego potęgowania wykorzystuje dwójkową postać wykładnika. Niech n w zapisie binarnym będzie k-cyfrową liczbą:

n = (n_k-1n_k-2...n₁n₀)₂, gdzie n_i ∈ {0,1} dla i=0,1,...,k-1

Wartość liczby n da się więc przedstawić w postaci sumy różnych potęg 2:

n = n₀ + 2·n₁ + 4·n₂ + 8·n₃ + ... + 2^k-1·n_k-1

Przedstawmy zatem xⁿ w następujący sposób:

xⁿ = x^{n₀ + 2·n₁
+ 2²·n₂ + ... + 2^k-1·n_k-1} = n₀·x¹ · n₁·x² · n₂·x⁴ · n₃·x⁸ · ... · n_k-1·x^{2^k-1}

Algorytm szybkiego potęgowania polega więc na iteracyjnym podnoszeniu do kwadratu kolejnych wartości począwszy od x i wymnażaniu tych, które odpowiadają bitom ustawionym na 1. Liczba obliczanych w tej metodzie iloczynów jest logarytmiczna względem wartości n. Oto schemat blokowy przedstawiający szybkie potęgowanie:

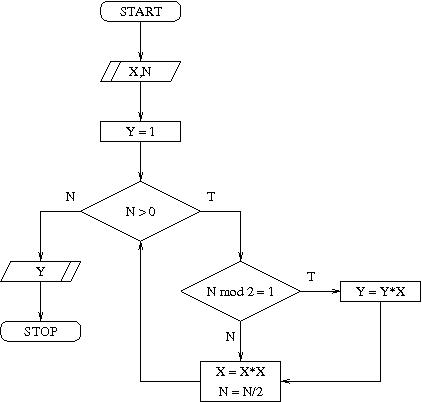
Budowa i działanie maszyny RAM

Kilka użytecznych linków:

Programy dla maszyny RAM

Jak się zabrać za napisanie programu dla maszyny RAM? Najlepiej postępować według sprawdzonej procedury:

wymyśl algorytm;
zapisz go w postaci schematu blokowego;
przetłumacz zawartość każdego bloku ze schematu na kod maszyny RAM;
poskładaj fragmenty programu w jedną całość i zapisz go w postaci jednego programu;
uruchom ten program i przetestuj jego działanie (w razie konieczności popraw błędy);
teraz można dokonać optymalizacji kodu (o ile jest to potrzebne).

24.09.2008: skoki w programach na maszynę RAM, przetwarzanie ciągów liczbowych

Sprawdzian

Narysuj schemat blokowy wyliczający funkcję sgn(x) dla zadanego x. Funkcja ta zwraca wartość -1 dla x<0, wartość 0 dla x=0 albo wartość +1 dla x>0.

Zadanie 1

Zadany jest ciąg złożony z liczb ujemnych i dodatnich. Koniec tego ciągu jest oznaczony na wartością 0. Narysuj schemat blokowy a potem na jego podstawie napisz program dla maszyny RAM, który odpowie czy w tym ciągu jest więcej liczb dodatnich czy ujemnych czy może jest ich tyle samo.

Zadanie 2

Zadany jest niepusty ciąg złożony z liczb ujemnych i dodatnich. Koniec ciągu jest oznaczony na wartością 0, która nie jest częścią tego ciągu. Narysuj schemat blokowy a potem na jego podstawie napisz program dla maszyny RAM, który:

wypisze maksymalną wartość w tym ciągu (nie uwzględniaj kończącego 0);
wypisze minimalną wartość w tym ciągu (nie uwzględniaj kończącego 0);
wypisze najpierw minimalną a potem maksymalną wartość w tym ciągu (nie uwzględniaj kończącego 0).

8.10.2008: operacja modulo, algorytm Euklidesa

Sprawdzian

Narysuj schemat blokowy wyznaczający medianę (wartość środkową po uporządkowaniu) spośród trzech zadanych liczb. Twój algorytm powinien dobrze pracować również wtedy, gdy dopuścimy możliwość powtarzania się wartości.

Operacja modulo na maszynie RAM

Bardzo często zachodzi potrzeba wyliczenia reszty z dzielenia. Na maszynie RAM nie ma rozkazu, który realizowałby takie działanie, dlatego należy napisać kod programu, który to oblicza.

Zadanie będzie więc polegało na napisaniu programu, który wyznaczy resztę z dzielenia dwóch liczb naturalnych a przez b. Przez a i b oznaczymy komórki z zadanymi liczbami a c będzie komórką na wynik. Do wyliczenia reszty z dzielenia za pomocą dostępnych na maszynie RAM rozkazów wykorzystamy zwykłe dzielenie całkowitoliczbowe, czyli rozkaz div. Najpierw a podzielimy przez b, potem wynik (bez części ułamkowej) pomnożymy przez b i liczbę którą otrzymamy odejmniemy od a, co da nam resztę z dzielenia. Oto program, który implementuje ten algorytm:

load a div b mult b sub a mult =-1 store c

Największy wspólny dzielnik

Dane są dwie liczby naturalne a i b, przy czym zakładamy, że a≥b>0. Zadanie polega na wyznaczeniu największego wspólnego podzielnika tych liczb d = NWD(a,b).

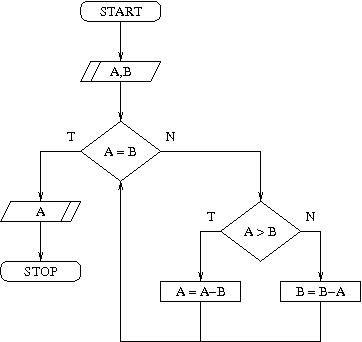
Algorytm naiwny sprawdzi po kolei wszystkich kandydatów. Kandydaci na NWD znajdują się w zbiorze {1,2,...,b}. Sprawdzanie najlepiej jest zacząć od największej liczby - sprawdzamy więc kolejno b, b-1, b-2,... Oto schemat blokowy przedstawiający takie naiwne podejście i program w języku maszyny RAM:

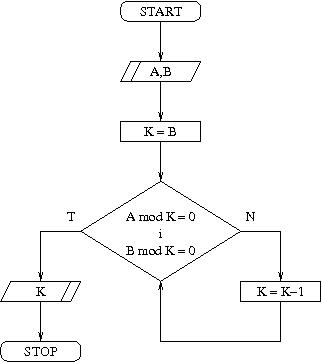; wczytywanie danych read 1 ; a to komórka 1 read 2 ; b to komórka 2 ; inicjalizacja licznika load 2 store 3 ; licznik c to komórka 3 ; sprawdzenie warunku petla: load 1 div 3 mult 3 sub 1 mult =-1 jgtz dalej load 2 div 3 mult 3 sub 2 mult =-1 jgtz dalej jump koniec ; zmniejszenie licznika dalej: load 3 sub =1 store 3 ; wypisanie wyniku koniec: write 3 halt

Uwaga! Koszt tego algorytmu może być bardzo duży. Dla liczb względnie pierwszych algorytm wykona pętlę aż b razy.

Algorytm trochę lepszy korzysta z następującego faktu:

Fakt 1:: Niech a, b i d będą liczbami naturalnymi, oraz niech a≥b. Wówczas, jeśli d | a i d | b, to d | (a-b).
Dowód:: Przedstawimy a i b w postaci iloczynów
a = d·x
b = d·y
gdzie x i y to liczby naturalne tak dobrane, aby były spełnione powyższe równości. Teraz wyliczymy różnicę a-b:
a-b = d·x-d·y = d·(x-y)
Wynika z tego, że przy spełnionych założeniach w implikacji d | (a-b), co kończy dowód.

Fakt ten pozwala zredukować problem znajdowania NWD(a,b) do problemu trochę mniejszego NWD(a-b,b). Sytuacja, w której a i b są równe jest trywialna, bo NWD(a,a) = a. Oto schemat blokowy przedstawiający metodę trochę lepszą:

Uwaga! Koszt tego algorytmu jest nieco lepszy od poprzedniego. Dla odpowiednio dobranych liczb algorytm wykona pętlę nawet a/b razy.

Algorytm Euklidesa, który jest znacznie lepszy od poprzednich, korzysta z faktu:

Fakt 2:: Niech a, b i d będą liczbami naturalnymi, oraz niech a≥b. Wówczas, jeśli d | a i d | b, to d | (a mod b).
Dowód:: Przedstawimy a i b w postaci iloczynów
a = d·x
b = d·y
gdzie x i y to liczby naturalne tak dobrane, aby były spełnione powyższe równości. Dalej niech
a mod b = m
czyli
a = b·z+m
gdzie z jest częścią całkowitą z a/b. Teraz za a i b podstawimy iloczyny:
m = a-b·z = d·x-d·y·z = d·(x-y·z)
Wynika z tego, że przy spełnionych założeniach w implikacji d | (a mod b), co kończy dowód.

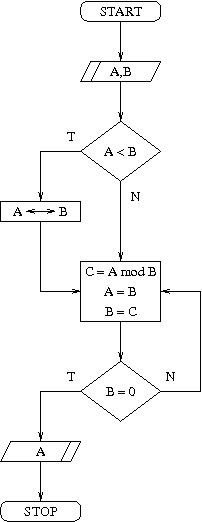
Fakt ten pozwala zredukować problem znajdowania NWD(a,b) do problemu istotnie mniejszego NWD(b,a mod b). Sytuacja, w której b=0 trywialna, gdyż NWD(a,0) = a. Oto schemat blokowy przedstawiający algorytm Euklidesa:

Uwaga! Koszt tego algorytmu jest dużo lepszy od poprzednich. Dla dowolnych liczb algorytm wykona pętlę co najwyżej 2·log₂(a) razy.

15.10.2008: binarna reprezentacja liczb w komputerach

Sprawdzian

Napisz program dla maszyny RAM, który wczyta jedną liczbę z taśmy wejściowej a następnie wyliczy i zapisze na taśmę wyjściową sumę cyfr tej liczby w rozwinięciu 10-tnym.

Zapis liczby w postaci dziesiętnej

Jesteśmy przyzwyczajeni do przedstawiania liczb naturalnych w systemie dziesiętnym. System ten pojawił się w Indiach w V w. skąd dotarł do Europy za pośrednictwem Arabów (dlatego cyfry tego systemu nazywamy cyframi arabskimi). W systemie tym występuje 10 różnych cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Za pomocą jednej cyfry można więc przedstawić dziesięć różnych wartości. To niewiele. Dlatego większe wartości zapisuje się za pomocą ciągu cyfr. Taki ciąg cyfr to liczba dziesiętna. Każda cyfra w liczbie reprezentuje inną wartość, z zależności od zajmowanej pozycji - ostatnia cyfra określa liczbę jedności, przedostatnia liczbę dziesiątek, przedprzedostatnia liczbę setek, itd.

Z każdą pozycją w liczbie dziesiętnej jest więc związana określona potęga 10: ostatnia pozycja to jedności czyli 10⁰, przedostatnia to dziesiątki czyli 10¹, przedprzedostatnia to setki czyli 10², itd. Niech dana będzie liczba d. Liczbę tą zapiszemy za pomocą k cyfr dziesiętnych (dla odpowiednio dobranego parametru k):
d = (d_k-1d_k-2...d₁d₀)
Wówczas wartość liczby d można wyznaczyć w następujący sposób:
d = d_k-1·10^k-1 + d_k-2·10^k-1 + ... + d₁·10¹ + d₀·10⁰
Można to zwięźle zapisać w następujący sposób:
d = ∑_i=0^k-1(d_i·10ⁱ)

Zapis liczby w postaci binarnej

Liczby można też zapisywać w innych systemach liczbowych. Popularnym systemem jest system dwójkowy, zwany też binarnym. System dwójkowy został spopularyzowany przez W.G.Leibniza w XVII w. W systemie tym występują tylko dwie cyfry: 0 i 1. Podobnie jak w dziesiętnym systemie pozycyjnym, liczby naturalne przedstawiamy jako sumę potęg 2 z odpowiednimi wagami reprezentowanymi przez cyfry 0 albo 1.

System dwójkowy jest obecnie bardzo popularny, głównie z powodu rozwoju elektroniki cyfrowej. Każda liczba w komputerze jest pamiętana w postaci dwójkowej. System dwójkowy został wybrany ze względów technologicznych. Łatwo jest bowiem rozróżnić dwie wartości, niż jakąkolwiek większą ich liczbę: wystarczy tylko rozróżnić "sygnał" od "braku sygnału", aby reprezentować dwie cyfry binarne.

W liczbie dwójkowej każda pozycja cyfry jest związana z określoną potęgą 2: ostatnia pozycja to jedności czyli 2⁰, przedostatnia to dwójki czyli 2¹, przedprzedostatnia to czwórki czyli 2², itd. Niech dana będzie liczba b. Liczbę tą można zapisać za pomocą k cyfr dwójkowych (dla odpowiednio dobranego parametru k):
b = (b_k-1b_k-2...b₁b₀)
Wówczas wartość liczby b można wyznaczyć w następujący sposób:
b = ∑_i=0^k-1(b_i·2ⁱ)

Pozostaje jeszcze kwestia, jak wyznaczyć poszczególne cyfry binarnej reprezentacji zadanej wartości. Idea jest dość prosta: dla zadanej liczby b wyznaczamy ostatnią cyfrę b₀ jej binarnej reprezentacji (ostatnia cyfra to b₀ = b mod 2), obcinamy ostatnią cyfrę z liczby (to będzie (b-b₀) / 2) i powtarzamy tą czynność (wyznaczając jej kolejne cyfry), aż osiągniemy wartość 0. Oto schemat blokowy ilustrujący tą metodę:

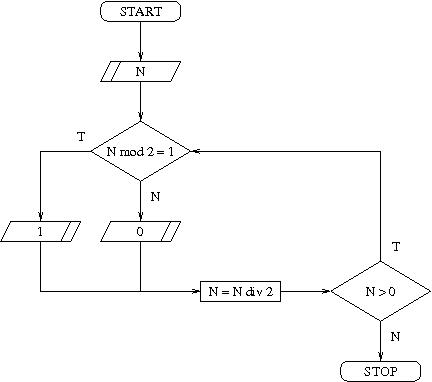
Zapis liczby w dowolnym systemie liczbowym

Liczby naturalne można zapisywać w systemach liczbowych o dowolnej podstawie r≥2. Poszczególne cyfry takiego zapisu wyznacza się podobnie jak w reprezentacji binarnej, tylko że zamiast operować 2, oblicza się iloraz i resztę z dzielenia przez r.

Zapytanie

Dana jest liczba naturalna x. Opisz metodę wyznaczenia jej kolejnych cyfr w zapisie dziesiętnym. Zaczynij od jedności.

Zadanie 1

Wczytaj liczbę naturalną x z taśmy wejściowej i wypisz kolejne cyfry x w postaci binarnej. Zaczynij od jedności.

Zadanie 2

Wczytaj liczbę naturalną x z taśmy wejściowej i wypisz kolejne cyfry x w postaci trynarnej. Zaczynij od jedności.

Zadanie 3

Wczytaj liczby naturalne r≥2 i x z taśmy wejściowej i wypisz kolejne cyfry reprezentacji x w systemie r-arnym zaczynając od jedności.

Zadanie 4

Wczytaj liczbę naturalną x z taśmy wejściowej i wypisz kolejne cyfry reprezentacji binarnej x zaczynając od najbardziej znaczącej cyfry.

Istnieje kilka pomysłów na rozwiązanie tego zadania. Pomysł Wojtka był taki, aby stablicować sobie wszystkie cyfry zaczynając od jedności a potem wypisać je od końca. Zaletą tego pomysłu jest prostota, ale wada jest oczywista - zużywamy dużo pamięci.

Pomysł Agaty, to wyznaczenie najbardziej znaczącej cyfry, poprzez znalezienie najmniejszej potęgi 2, liczby k, takiej że 2^k > x. No to z tego wynika, że do zapisu liczby x potrzebujemy k cyfr binarnych oraz że cyfra na pozycji (k-1)-szej jest jedynką. Zaczynając więc od pozycji (k-1)-szej wyznaczamy kolejne cyfry tej liczby i kończymy na cyfrze jedności. Oto schemat blokowy dla tego algorytmu:

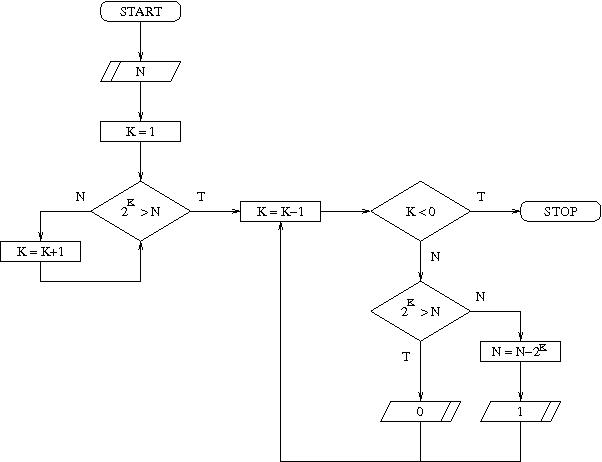
22.10.2008: przetwarzanie tablic na maszynie RAM

Sprawdzian

Narysuj schemat blokowy i na jego podstawie napisz program dla maszyny RAM, który wczyta jedną liczbę z taśmy wejściowej a następnie obliczy i zapisze na taśmę wyjściową rozkład tej liczby na czynniki pierwsze.

Zadanie 1

Wczytaj liczbę naturalną x z taśmy wejściowej i wypisz kolejne cyfry reprezentacji binarnej x zaczynając od najbardziej znaczącej cyfry. Wszystkie cyfry wpisz najpierw do tablicy przed ich wypisaniem.

Tablica to struktura danych, w której można pamiętać wiele liczb. Zajmuje ona spójny obszar w pamięci. Komórki w tablicy są ponumerowane kolejnymi liczbami całkowitymi. Przyjmuje się, że pierwsza komórka ma numer 0, druga numer 1, itd. Numery tych komórek nazywane są indeksami. Jeśli chcemy odwołać się do komórki o indeksie j w tablicy T, to odwołanie takie zapisujemy jako T_j albo T[j].

W maszynie RAM istnieje wygodny mechanizm odwoływania się do komórek tablicy za pomocą adresowania pośredniego. W określonej komórce pamięci, nazwijmy ją p, można przechowywać numer komórki pamięci, do której chcemy się odwołać. Jeśli w komórce pamiętamy adres innej komórki pamięci, to nazywamy ją wskaźnikiem. Aby owołać się do komórki, której adres jest przechowywany we wskaźniku p, to w programie argument taki zapisujemy jako ^p.

W programach dla maszyny RAM wygodnie jest używać trzech komórek pamięci do indeksowania elementów tablicy. Niech j będzie komórką, w której przechowujemy indeks elementu w tablicy; w T będziemy pamiętali adres komórki pamięci, w której tablica ma swój początek (pierwszy element o indeksie 0); natomiast do komórki i wyliczymy i wpiszemy adres j-tej komórki w tablicy T. Jak się wykorzystuje taką trójkę przy czytaniu i pisaniu do tablicy pokazuje poniższy przykład.

; wczytanie do akumulatora wartości z j-tej komórki z tablicy load j add T store i load ^i ; zapisanie wartości z akumulatora do j-tej komórki w tablicy store tmp load j add T store i load tmp store ^i

Wróćmy teraz do zadania i do pomysłu Wojtka na jego rozwiązanie. Idea jest taka, że wyliczamy kolejne cyfry liczby x zaczynając od jedności i wpisujemy je do tablicy; gdy już mamy stablicowane wszystkie cyfry, to wypisujemy je od końca. Oto schemat blokowy i program dla tego algorytmu:

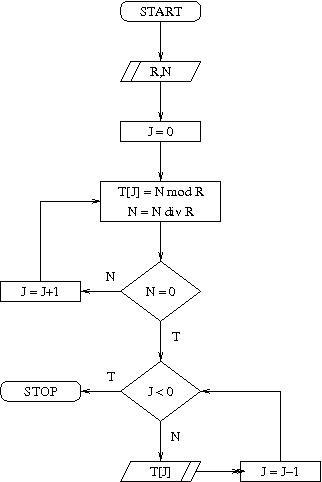; in >> R >> N read 1 ; R to komórka 1 read 2 ; N to komórka 2 ; inicjalizacja ; T <- 10 ; wskaźnik na początek tablicy ; J <- 0 ; indeks komórki w tablicy ; I <- 0 ; adres indeksowanej komórki ; TMP to komórka 8 load =10 store 4 load =0 store 5 load 4 store 6 ; T[J] <- N mod R ; N <- N div R petla1: load 2 div 1 mult 1 sub 2 mult =-1 store 8 load 5 add 4 store 6 load 8 store ^6 load 2 div 1 store 2 ; czy N=0 load 2 jzero dalej jump petla2 ; J++ dalej: load 5 add =1 store 5 jump petla1 ; czy J<0 petla2: load 5 mult =-1 jgtz koniec ; out << T[J] load 5 add 4 store 6 load ^6 write 0 ; J-- load 5 sub =1 store 5 jump petla2 koniec: halt

Jeśli w programie dla maszyny RAM potrzebujemy skorzystać z tablicy, której wielkości nie można z góry określić, to należy zaplanować jej położenie w pamięci operacyjnej na końcu, za wszystkimi innymi wykorzystywanymi komórkami pamięci.

Zadanie 2

Liczbę nazywamy palindromiczną, gdy jej zapis w określonym systemie liczbowym jest palindromem. A palindrom to taki ciąg znaków, który czytany wspak jest taki sam jak czytany normalnie. Przykłady znanych palindromów w języku polskim to: kajak, Anna, kobyła ma mały bok, Zakopane na pokaz, może jutro ta Dama da tortu jeżom. Przykłady liczb palindromicznych w systemie dziesiętnym to: 1, 22, 34543, 9867007689.
Wczytaj liczbę naturalną x z taśmy wejściowej i sprawdź czy jest ona palindromiczna w systemie dziesiętnym. Na taśmę wejściową zapisz 1 gdy x jest liczbą palindromiczną albo 0 gdy nie jest.

Istnieje kilka sposobów na rozwiązanie tego zadania. Jednym z nich jest stablicowanie wszystkich cyfr zadanej liczby a potem sprawdzenie czy cyfry na odpowiadających sobie pozycjach są takie same - porównujemy kolejne cyfry, pierwszą cyfrę z ostatnią, drugą z przedostatnią, itd. Jeśli wszystkie porównania miały odpowiedź twierdzącą, to liczba jest palindromiczna.

Inny sposób polega na odwróceniu liczby, czyli takim przekształceniu aby w zapisie dziesiętnym nowa liczba czytana wspak była taka sama jak liczba pierwotna czytana normalnie. Jeśli obie liczby mają taką samą wartość, to liczba jest palindromiczna. Ten pomysł można zrealizować bez używania tablicy.

29.10.2008: wprowadzenie do języka C++: we/wy, zmienne, wyrażenia, instrukcje

Notatki w sieci dotyczące programowania w języku C

Kilka użytecznych linków:

Bardzo szybkie wprowadzenie do programowania w języku C w można znaleźć w notatkach K.Lorysia uzupełnionych przez R.Nowaka (IntroC.doc).
Dość wyczerpujący opis języka C jest dostępny na pl.wikibooks.org/wiki/C, a do tego wszystkiego jest książka w wersji elektronicznej (C.pdf).

Wprowadzenie do języka C/C++

struktura programu w języku C
standardowe wejście i wyjście
deklarowanie zmiennych
operatory arytmetyczne
instrukcja warunkowa if / if-else
operatory porównań
pętle while i do-while

Struktura programu w języku C

Jak pisze się programy w języku C? Język C jest językiem proceduralnym, co oznacza, że definiuje się w nim procedury, zazywane zwyczajowo funkcjami. Funkcja jest sekwencją instrukcji, która realizuje określone zadanie. Funkcje powinny być krótkie, proste i napisane czytelnie, aby zapisany w nich kod był jasny dla innych programistów. Zaleca się też pisanie komentarzy wyjaśniających pewne bardziej skomplikowane obliczenia.

Program dla maszyny RAM był ciągiem instrukcji, każda zapisana w osobnej linii. W języku C programów tak się nie pisze. Program to zbiór definicji funkcji, a każda funkcja definiuję sekwencję instrukcji. W programie musi się pojawić definicje funcji main(), ponieważ od wywołania tej funkcji program rozpoczyna swoje działanie.

Czym różni się język C od C++? Jeżyk C to język proceduralny, a C++ jest obiektowy - można w nim oprócz funkcji definiować własne klasy. Nie będziemy zajmowali się na tych zajęcich programowaniem obiektowym, ale będziemy korzystali z już zdefiniowanych w bibliotece standardowej obiektów. Oto przykład prostego programu powitalnego, napisanego w C++:

# include <string> # include <iostream> using namespace std; int main () { cout << "Witaj na lekcji informatyki!" << endl; cerr << "Podaj swoje imię: "; string im; cin >> im; cout << "Cześć " << im << "!!!" << endl; return 0; }

Co w tym prostym programie się znajduje? Pierwsze dwie linie to włączenie plików nagłówkowych <string> i <iostream> z deklaracjami wybranych funkcji i klas z biblioteki standardowej. Trzecia linijka to deklaracja użycia przestrzeni nazw std - powinna się ona zawsze pojawić po włączeniu plików nagłówkowych. A potem jest zdefiniowana funkcja main() - po nagłówku funkcji następuje ciąg instrukcji i deklaracji ujęty w nawiasy klamrowe. Działanie tego programu polega na wypisaniu komunikatu powitalnego, zapytaniu o imię i imiennym powitaniu użytkownika.

Biblioteka standardowa

Biblioteka standardowa to olbrzymi zbiór definicji różnego rodzaju funkcji i klas. Biblioteka ta została podzielona tematycznie na małe części i dla każdego takiego fragmentu napisano tak zwany plik nagłówkowy zawierający deklaracje zapowiadające wybranych funkcji i klas.

W pliku nagłowkowym <string> zdefiniowano klasę string, której obiekty służą do przechowywania łańcuchów znakowych (napisów) i manipulowania nimi.

W pliku nagłowkowym <iostream> są zadeklarowane obiekty związane ze standardowym wejściem (klawiatura) i wyjściem (monitor). Obiekt cin jest związany ze strunieniem wejściowym i służy do wczytywania danych do programu za pomocą operatora >>. Do pisania na standardowe wyjście jest przeznaczony obiekt cout a na standardowe wyjście dla błędów obiekt cerr. Strumienie wyjściowe posługują się operatorem << do posyłania danych na wyjście. Obydwa strumienie wyjściowe cout i cerr piszą na monitorze, istnieje jednak subtelna różnica między nimi - generalnie obiektu cout używamy do wypisywania ostatecznych wyników działania programu a cerr do wybisywania komentarzy i komunikatów pomocniczych.

Często korzysta się też z plików nagłówkowych <cstdlib> i <cmath> gdzie zadeklarowane są różne funkcje matematyczne.

Zadanie 1

Napisz program, który wczyta liczbę lat a potem wyliczy i wypisze ile to miesięcy i dni.

Zadanie 2

Napisz program, który wczyta dwie liczby a potem wyliczy i wypisze maksimum z tych liczb. Zastosuj instrukcję warunkową.

Zadanie 3

Napisz program, który wczyta liczbę n a potem wyliczy i wypisze kwadraty kolejnych liczb naturalnych 1², 2², 3², ...,n². Zastosuj instrukcję pętli.

12.11.2008: wprowadzenie do języka C++: instrukcje, tablice

Sprawdzian

Napisz program, który wczyta liczbę całkowitą 1≤n≤20 a potem wydrukuje trójkąt złożony za znaków '*' tak jak w poniższym przykładzie (dla n=5): * * * * * * * * * * * * * * *

Wprowadzenie do języka C/C++

pętla for
instrukcje break i continue
manipulatory setw i setfill
zagnieżdżanie pętli
tablice jednowymiarowe w języku C

Zadanie 1

Napisz program, który wczyta liczbę całkowitą 1≤n≤20 a potem wydrukuje trójkąt złożony za znaków '*' tak jak w poniższym przykładzie (dla n=5): * * * * * * * * * * * * * * *

Zadanie 2

Napisz program, który wczyta liczbę całkowitą n>0 a potem ciąg liczb całkowitych a₀, a₁, ..., a_n-1, umieści je w automatycznie utworzonej tablicy i wypisze od końca.

Tablicę można utworzyć dopiero wtedy gdy bedziemy znali jej rozmiar. W tym programie najpierw wczytamy rozmiar tablicy a potem ją utworzymy i wypełnimy danymi.

# include <iostream> # include <iomanip> using namespace std; int main () { cerr << "n = "; int n; cin >> n; int tab[n]; for (int i=0; i<=n-1; i++) { cerr << "a[" << i << "] = "; cin >> tab[i]; } for (int j=n-1; j>=0; j--) cout << setw(10) << tab[j] << endl; return 0; }

Zadanie 3

Napisz program, który wczyta liczbę całkowitą n>0 a potem wypisze tę liczbę w postaci trójkowej. Stablicuj cyfry rozwinięcia trójkowego zadanej liczby.

Zadanie 4

Napisz program, który wczyta liczbę całkowitą n>0 a potem policzy wypisze ile ta liczba ma cyfr 0, 1 i 2 w zapisie trójkowym. Nie tablicuj cyfr rozwinięcia trójkowego zadanej liczby.

19.11.2008: wprowadzenie do języka C++: funkcje

Sprawdzian

Napisz program, który wczyta trzy dodatnie liczby całkowite x, y i z a potem jeszcze dwie a≤b wyznaczające przedział liczbowy <a,b> a potem wyliczy i wypisze ile liczb z tego przedziału jest podzielnych przez x lub y lub z.

Funkcje w języku C/C++

podział programu na procedury obliczeniowe
deklaracja funkcji
definicja funkcji
parametry wejściowe funkcji
wynik zwracany przez funkcję i instrukcja powrotu z funkcji return
wywołanie funkcji

Zadanie 1

Dane są liczby naturalne x>0 i c. Ile jest liczb z przedziału <1,c>, które są podzielne przez x?

Rozwiązując to zadanie, może lepiej jest najpierw postawić pytanie: jakie to są liczby? Odpowiedź wydaje się oczywista - wszystkie wielokrotności x, które są ≤c, czyli x, 2x, 3x... No to teraz pytanie: ile jest tych wielokrotności? Jest ich k, przy czym k jest takie, że kx≤c<(k+1)x. Tak więc k = ⌊c/x⌋.

Zadanie 2

Uogólnienie poprzedniego zadania do przedziału liczbowego. Dane są liczby naturalne x>0 oraz a i b, gdzie a≤b. Ile jest liczb z przedziału <a,b>, które są podzielne przez x?

Będziemy bazować na rozwiązaniu poprzedniego zadania. Wiemy, że jest ⌊b/x⌋ liczb z przedziału <1,b> podzielnych przez x oraz ⌊(a-1)/x⌋ liczb z przedziału <1,a-1> podzielnych przez x. No więc w przedziale <a,b> liczb podzielnych przez x jest ⌊b/x⌋ - ⌊(a-1)/x⌋.

Zadanie 3

Uogólnienie poprzedniego zadania do dowolnego przedziału. Dane są liczby całkowite x>0 oraz a i b, gdzie a≤b. Ile jest liczb z przedziału <a,b>, które są podzielne przez x?

Będziemy bazować na rozwiązaniu poprzedniego zadania...

26.11.2008: wprowadzenie do języka C++: funkcje i rekurencja

Sprawdzian

Napisz program, który wczyta liczbę całkowitą x>0, a potem wyliczy i wypisze informację o tym, czy w liczbie x w zapisie dziesiętnym jest więcej cyfr parzystych (odpowiedź 0), nieparzystych (odpowiedź 1) czy jest ich tyle samo (odpowiedź -1).

Zadanie 1

Napisz program, który wczyta liczbę całkowitą x>0, a potem wyliczy i wypisze ile różnych liczb można utworzyć wykorzystując wszystkie cyfry dziesiętnego zapisu liczby x. W swoim programie zdefiniuj i wykorzystaj funkcję obliczającą silnię: int silnia (int);

Rozwiązaniem zadania jest liczba możliwych kombinacji złożonych z określonej liczby cyfr dziesiętnych. Cyfry mogą się powtarzać i są nierozróżnialne. Gdybyśmy mieli k różnych cyfr, to rozwiązaniem byłaby wartość k!. W ogólnym przypadku wyliczamy liczbę poszczególnych cyfr: k₀ to liczba zer, k₁ jedynek itd; wartość k można więc zapisać za pomocą sumy k = k₀+k₁+...+k₉. Liczba wszystkich kombinacji z uwzględnieniem powtórzeń wynosi k! / (k₀!·k₁!·...·k₉!).

Rozwiązując to zadanie zdefiniowaliśmy funkcję, która oblicza n! (przypomnienie: n! = n·(n-1)·...·2·1):

int silnia (int n) { int s = 1; while (n>1) s *= n--; return s; }

Rekurencja

Rekurencja (ang. recursion; łac. recurrere, przybiec z powrotem) to w logice i w matematyce odwoływanie się definicji lub funkcji do samej siebie. Przykładem definicji rekurencyjnej może być właśnie funkcja silni:
0! = 1
1! = 1
2! = 2·1 = 2
3! = 3·2·1 = 6
n! = n·(n-1)·...·2·1 = n·(n-1)! dla n≥1
Rekurencyjny wzór na obliczenie n! zapisuje się w następujący sposób: n! = n·(n-1)!. Ze wzoru tego wynika, że aby obliczyć na przykład 4!, należy najpierw obliczyć 3!, żeby obliczyć 3! trzeba obliczyć 2! itd, aż dojdziemy do 0!, które wynosi 1 jak wynika z definicji.

W programowaniu mówimy o funkcjach rekurencyjnych, gdy w ich definicji następuje wywołanie tej samej funkcji. Ważnym elementem programowania funkcji rekurencyjnych jest warunek wyjścia z rekurencji, czyli taka wartość dla której można udzielić odpowiedzi ad hoc. Oto przykład rekurencyjnej definicji funkcji obliczającej silnię:

int silnia (int n) { if (n<2) return 1; // warynek wyjścia z rekurencji return n*silnia(n-1); }

Zadanie 2

Napisz program rozwiązujący zadanie z Czesiem pokonującym schody. W swoim programie zdefiniuj funkcję rekurencyjną obliczająca n-tą liczbę Fibonacciego.

Oto funkcja rekurencyjna obliczająca n-tą liczbę Fibonacciego:

int fib (int n) { if (n<2) return n; return fib(n-1)+fib(n-2); }

Czasem rekurencja jest zgubna! Funkcje rekurencyjne pisze się bardzo prosto, przenosząc niemal definicję matematyczną do programu. Ale rekurencja wymaga od nas dodatkowej pamięci i czasu potrzebych dla każdego wywołania rekurencyjnego.

Można udowodnić (dowód przez indukcję), że wyliczając liczbę Fibonacciego za pomocą funkcji rekurencyjnej przedstawionej powyżej jest wykładniczo duża! Jeśli funkcję tą uruchomimy z parametrem n>2, to liczba rekurencyjnych wywołań tej funkcji w czasie obliczeń jest >2^n/2.

Zadanie 3a

Napisz program, który wczyta liczbę całkowitą 1≤n≤20 a potem wydrukuje trójkąt złożony za znaków '0', '1' i '2' tak jak w poniższym przykładzie (dla n=5): 0 1 2 0 1 2 0 1 2 0 1 2 0 1 2

Zadanie 3b

Napisz program, który wczyta dwie liczby całkowite n i k, takie że 1≤k≤n≤10⁹, a potem wyliczy i wypisze cyfrę jaka jest zapisana w trójkącie złożonym ze znaków '0', '1' i '2' wydrukowanego według schematu opisanego powyżej.

3.12.2008: wprowadzenie do języka C++: typy danych

Sprawdzian: Robotnicy budowlani wykopali rów długości n metrów. Do jego wykopania użyto specjalnej koparki, która wybierała ziemię fragmentami co metr. Ponieważ operator koparki, pan Czesław, dopiero przyuczył sie do zawodu, więc wykopał on rów ale nierówny - poszczególne fragmenty rowu mają różną głębokość. W nocy spadł ulewny deszcz, cały rów został zalany i teraz trzeba go osuszyć poprzez wypompowanie z niego wody. Napisz program, który wczyta liczbę całkowitą n>0, potem głębokości poszczególnych 1-metrowych fragmentów rowu g₀, g₁,... g_n-1, a na koniec wyliczy i wypisze jaka jest minimalna liczba pomp potrzebna do wypompowania wody z tego rowu.

10.12.2008: wprowadzenie do języka C++: wskaźniki

Sprawdzian: Dany jest n-elementowy cią liczb a₀, a₁, ..., a_n-1. Należy w tym ciągu znaleźć taki spójny podciąg rosnący, w którym różnica między pierwszym a ostatnim elementem będzie maksymalna. Rozwiązaniem jest wartość tej różnicy.

powrót na początek strony

Zadania domowe

Zadanie 1

Zadanie

Wyznacz wartość x w następujący sposób:

x = 100 + twój numer w dzienniku

Następnie oblicz x-ty wyraz ciągu Fibonacciego F_x, wykorzystując do tego celu maszynę RAM.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
wartość x wyznaczona w podany wyżej sposób;
wartość x-tej liczby Fibonacciego F_x;
program na maszynę RAM, który oblicza x-ty wyraz ciągu Fibonacciego (wykorzystaj metodę iteracyjną).

Wysyłając list wpisz w tytule 14 LO - zadanie 1.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 22 września 2008 r. o godzinie 23:59.

Zadanie 2

Zadanie

Zadany jest niepusty ciąg złożony z liczb ujemnych i dodatnich. Koniec ciągu jest oznaczony na wartością 0, która nie jest jego częścią. Narysuj schemat blokowy a potem na jego podstawie napisz program dla maszyny RAM, który:

obliczy sumę wszystkich wyrazów tego ciągu;
obliczy iloczyn wszystkich wyrazów tego ciągu;
obliczy średnią arytmetyczną zaokrągloną w dół wszystkich wyrazów tego ciągu (zaokrąglenie jest wynikiem działania maszyny RAM, która wykonuje dzielenie całkowitoliczbowe ucinając część ułamkową).

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
programy na maszynę RAM, które rozwiązują opisane zadania.

Wysyłając list wpisz w tytule 14 LO - zadanie 2.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 29 września 2008 r. o godzinie 23:59.

Zadanie 3

Zadanie

Liczba pierwsza p to liczba naturalna większa od 1, która ma dokładnie dwa dzielniki naturalne: 1 i p. Jeśli liczba naturalna jest większa od 1 i nie jest pierwsza, to nazywamy ją liczbą złożoną. Oto kilka początkowych liczb pierwszych: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Udowodnij, że jeśli liczba x jest złożona, to istnieje jakiś jej dzielnik pierwszy p, taki że p≤x^1/2.
Wykorzystaj powyższy fakt, do skonstruowania efektywnego algorytmu testującego pierwszość liczb, który wykona nie więcej niż x^1/2 dzieleń modulo dla zadanej liczby x. Napisz program na maszynę RAM, który implementuje ten algorytm; zakładamy, że na taśmie wejściowej będzie zapisana tylko jedna liczba, a na taśmie wyjściowej ma zostać wypisany największy dzielnik tej liczby.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
dowód faktu o najmniejszym dzielniku pierwszym liczby złożonej;
program na maszynę RAM, który testuje pierwszość zadanej liczby.

Wysyłając list wpisz w tytule 14 LO - zadanie 3.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 13 października 2008 r. o godzinie 23:59.

Zadanie dodatkowe A

Zadanie :-)

Czesio ma do pokonania n>0 schodów. Czesio nie ma długich nóg, więc może pokonywać schody przechodząc dalej o 1, 2 albo 3 stopnie. Chciałby też codziennie przechodzić je inaczej. Pomóż Czesiowi obliczyć, przez ile dni będzie mógł pokonywać schody w inny sposób.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
wzór rekurencyjny według którego można obliczać liczbę sposobów na pokonanie przez Czesia schodów dla kolejnych wartości n;
macierz transformacji w algorytmie macierzowym rozwiązującym to zadanie;
program na maszynę RAM, który rozwiązuje to zadanie (użyj metody iteracyjnej albo macierzowej).

Wysyłając list wpisz w tytule 14 LO - zadanie dodatkowe A.

Punkty

Za rozwiązanie tego zadania metodą iteracyjną można otrzymać 10 punktów a za rozwiązanie metodą macierzową 20.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 13 października 2008 r. o godzinie 23:59.

Zadanie 4

Zadanie

Napisz program na maszynę RAM, który wczyta jedną liczbę z taśmy wejściowej i zapisze na taśmie wyjściowej kolejne cyfry binarnej reprezentacji tej liczby zaczynając od cyfry najbardziej znaczącej a kończąc na cyfrze jedności. Zaimplementuj algorytm przedstawiony na lekcji przez Agatę.
Wykaż, że ten algorytm działa poprawnie. Udowodnij, że dla dowolnej liczby naturalnej x jeśli 2^k > x ∧ 2^k-1 ≤ x, to do zapisu binarnego liczby x potrzebnych jest k cyfr oraz na pozycji (k-1)-szej znajduje się 1 (pozycje cyfr w liczbie są numerowane od 0 i cyfra jedności znajduje się właśnie na pozycji 0).

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
uzasadnienie, że algorytm opisany przez Agatę działa poprawnie;
program na maszynę RAM, który wypisuje odczytaną liczbę w postaci binarnej.

Wysyłając list wpisz w tytule 14 LO - zadanie 4.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 20 października 2008 r. o godzinie 23:59.

Zadanie 5

Zadanie

Napisz program dla maszyny RAM, który wczyta liczbę naturalną x>3 z taśmy wejściowej i sprawdzi czy jest ona palindromiczna w jakimkolwiek systemie liczbowym o podstawie r, przy czym 2≥r≥x-2. Na taśmę wyjściową zapisz najmniejsze znalezione r, dla którego x zapisane w systemie r-arnym jest liczbą palindromiczną albo wartość 0 gdy takie r nie istnieje.
Uruchom twój program dla wszystkich liczb z zakresu 4...30 i napisz mi, które z nich są palindromiczne.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
listę wszystkich liczb palindromicznych z zakresu 4...30;
program na maszynę RAM, który sprawdza czy wczytana liczba jest palindromiczna.

Wysyłając list wpisz w tytule 14 LO - zadanie 5.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 27 października 2008 r. o godzinie 23:59.

Zadanie 6

Zadanie

Napisz program w języku C++, który wczyta liczbę n a potem sprawdzi czy n jest liczbą pierwszą i wypisze odpowiedni komunikat na standardowym wyjściu.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
program w języku C++, który sprawdza czy wczytana liczba jest pierwsza.

Wysyłając list wpisz w tytule 14 LO - zadanie 6.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 3 listopada 2008 r. o godzinie 23:59.

Zadanie 7

Zadanie

Napisz program, który wczyta ze standardowego wejścia liczbę całkowitą n>0 a potem ciąg liczb całkowitych a₀, a₁, ..., a_n-1, umieści je w automatycznie utworzonej tablicy a potem wyznaczy wartość i pozycję elementu maksymalnego (jeśli elementów o wartościach maksymalnych jest więcej niż jeden w tablicy to rozwiązaniem ma być pozycja najmniejsza) i wypisze wypisze te informacje na standardowe wyjście.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
program w języku C++, który wyznacza wartość i pozycję elementu maksymalnego w zadanym ciągu.

Wysyłając list wpisz w tytule 14 LO - zadanie 7.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 17 listopada 2008 r. o godzinie 23:59.

Zadanie 8

Zadanie

Napisz program, który wczyta ze standardowego wejścia liczbę całkowitą n>0 a potem wypisze największą liczbę zbudowaną z tych samych cyfr co n (w systemie dziesiętnym).
Wskazówka: policz ile poszczególnych cyfr w systemie dziesiętnym jest zawartych w liczbie n.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
program w języku C++, który wypisuje maksymalną liczbę złożoną z tych samych cyfr co n.

Wysyłając list wpisz w tytule 14 LO - zadanie 8.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 24 listopada 2008 r. o godzinie 23:59.

Zadanie 9

Zadanie :-)

Czesio ma do pokonania n>0 schodów. Czesio nie ma długich nóg, więc może pokonywać schody przechodząc dalej o 1, 2 albo 3 stopnie, przy czym nie może pokonać 3 stopni dwa razy pod rząd; dodatkowo jak się rozpędzi, to za pierwszym razem może (ale nie musi) przeskoczyć 4 lub 5 schodów. Chciałby też codziennie przechodzić je inaczej. Pomóż Czesiowi obliczyć, przez ile dni będzie mógł pokonywać schody za każdym razem w inny sposób.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
wzory rekurencyjne według których można obliczać liczbę sposobów na pokonanie przez Czesia schodów dla kolejnych wartości n; napisz uzasadnienie, skąd taki wzór się bierze;
program w języku C++, który wczyta z ilu stopni składają się schody a potem wyliczy i wypisze na ile sposobów Czesio może pokonać te schody (zaprogramuj odpowiednie funkcje rekurencyjne do rozwiązania tego zadania).

Wysyłając list wpisz w tytule 14 LO - zadanie 9.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 1 grudnia 2008 r. o godzinie 23:59.

Zadanie dodatkowe B

Zadanie

Napisz program, który wczyta trzy liczby całkowite 1≤x≤9 oraz n i k, takie że 1≤k≤n≤10⁹, a potem wyliczy i wypisze cyfrę jaka jest zapisana w wierszu n-tym na pozycji k-tej w trójkącie złożonym ze znaków '0', '1', ... i 'x' wydrukowanego według schematu opisanego z zadaniu na lekcji.
Przykład trójkąta dla x=3 i n=10: 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2 3 0 1 2
Uwaga! Zadanie to można rozwiązać w stałym czasie, zakładając że x jest pewną stałą!

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
krótki opis rozwiązania;
program w języku C++, który wypisuje cyfrę jaka jest zapisana w trójkącie złożonym x+1 cyklicznie powtarzających się cyfr (według schematu opisanego wyżej).

Wysyłając list wpisz w tytule 14 LO - zadanie dodatkowe B.

Punkty

Za rozwiązanie tego zadania można otrzymać 15 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 1 grudnia 2008 r. o godzinie 23:59.

Zadanie dodatkowe C

Zadanie

Niech dana będzie liczba rzeczywista x≥1. Skonstruujemy ciąg zbieżny do x^1/2 w podobny sposób jak na lekcji:
a₀ = x
a_i = (x/a_i-1+a_i-1)/2 dla i=1,2,3,...
Twoim zadaniem będzie wykazanie, że ciąg ten rzeczywiście zbiega do pierwiastka kwadratowego z x, czyli że kolejne wyrazy tego ciągu a_i są coraz bliższe x^1/2. Na ostatniej lekcji wykazaliśmy to w sposób eksperymentalny, pisząc odpowiedni program w języku C++. Teraz należy wykazać w sposób matematyczny, że właściwość ta jest prawdziwa.

Rozwiązanie

Rozwiązanie zadania należy spisać na kartce papieru formatu A4 i oddać mi je na początku najbliższych zajęć 10 grudnia. W rozwiązaniu zadania powinny się znaleźć następujące informacje:

imię i nazwisko;
dowód faktu, że a_i>1 dla wszystkich i=0,1,2,...;
dowód faktu, że a_i-1<a_i dla wszystkich i=1,2,3,...;
dowód faktu, że a_i>x^1/2 dla wszystkich i=0,1,2,...;
dowód twierdzenia, że kolejne wyrazy ciągu a_i są coraz bliższe x^1/2.

Dowody faktów przeprowadź indukcyjnie. Najpiękniejszy będzie dowód twierdzenia, bo musisz wymyśleć sposób na pokazanie, że odległość kolejnych wyrazów ciągu a_i od wartości x^1/2 maleje (wskazówka: przedstaw każdy wyraz ciągu a_i w postaci α_i·x^1/2, gdzie współczynniki α_i>1).

Punkty

Za rozwiązanie tego zadania można otrzymać 15 punktów.

Termin

Termin oddawania rozwiązań upływa w środę 10 grudnia 2008 r. o godzinie 7:45.

Zadanie 10

Zadanie

W zadaniu tym należy maksymalnie wykorzystać wskaźniki.

Zdefiniuj funkcję (taką jak na lekcji), która będzie zamieniała miejscami wartości wskazanych zmiennych typu int:
void zamiana (int *a, int *b);
Zdefiniuj funkcję, która określi pozycję elementu maksymalnego w zadanej tablicy:
int * pozycja_maks (int tab[], int n);
Zdefiniuj funkcję, która posortuje elementy w zadanej tablicy, wykorzystując metody zdefiniowane wcześniej. Sortowanie to powinno działać według następującego schematu: w tablicy n-elementowej określ pozycję elementu maksymalnego i zamień ten element z ostatnim (w ten sposób na końcu wyląduje element największy, cały problem zredukuje się więc o 1 element); powtórz taką samą czynność dla tablicy o jeden element krótszej (pomijając ostatni element); postępuj tak dopóki rozmiar tablicy jest większy od 1. Opisany algorytm porządkowania nosi nazwę sortowania przez wybieranie (bo wybieramy element największy i przenosimy go na koniec redukując problem). Zdefiniuj funkcję implementującą ten algorytm:
void sort_przez_wybor (int tab[], int n);
Napisz program, który wczyta ze standardowego wejścia liczbę całkowitą n>0 a potem ciąg liczb całkowitych a₀, a₁, ..., a_n-1, umieści je w automatycznie utworzonej tablicy, wypisze jej pierwotną zawartość, posortuje ją (korzystając ze zdefiniowanej wcześniej funkcji sortującej) i na końcu wypisze ją po uporządkowaniu.

Rozwiązanie

Rozwiązanie zadania należy przesłać do mnie mailem. W treści listu należy powinny się znaleźć następujące informacje:

imię i nazwisko;
program sortujący zadany ciąg wejściowy.

Wysyłając list wpisz w tytule 14 LO - zadanie 10.

Punkty

Za rozwiązanie tego zadania można otrzymać 10 punktów.

Termin

Termin nadsyłania rozwiązań upływa w poniedziałek 15 grudnia 2008 r. o godzinie 23:59.

powrót na początek strony