Wszystko co chciałbyś wiedzieć o labiryntach ale boisz się zapytać
Wiktor Zychla
Labirynt wygenerowany programem TorqMaze 0.02
Ściągnij źródło i binarium programu TorqMaze 0.02 (C#)
Ściągnij źródło i binarium programu TorqMaze 0.01 (C#)
Jeśli masz jakieś pytania lub uwagi na
temat tego artykułu: napisz do mnie.
W jaki sposób szybko i efektywnie budować labirynty?
W jaki sposób szybko i efektywanie znajdować drogę w labiryncie?
Problemom tym postanowiłem poświęcić kilka dni, ten artykuł zaś jest wynikiem owej kilkudniowej przygody.
Budowanie labiryntu
Algorytm budowania labiryntu jest bardzo intuicyjny. Zaczynamy od układu, w którym nie ma żadnych dróg
pomiędzy komórkami labiryntu, każda komórka otoczona jest czterema ścianami. Taki układ będę nazywał
zaczynem labiryntu lub po prostu zaczynem.
Algorytm polega na sprytnym przejściu całego zaczynu i decydowaniu o ewentualnym usuwaniu ścian dzielących
komórki. Z tego powodu jest niezykle szybki, działa w czasie liniowym.
Podsumujmy. Algorytm więc:
- jednokrotnego przejścia prostokątnego obszaru zaczynu w sposób losowy
- w każdym kroku przejścia - decydowania o tym czy usuwać ścianę dzielącą komórki czy nie
Losowe przechodzenie zaczynu obszaru
Losowe przejście zaczynu można dość łatwo przełożyć na algorytm rekurencyjny:
przechodz_komorki( x, y )
{
jesli ( odwiedzona( x, y ) ) return;
tworz_losowa_permutacje( p )_zbioru_0_3
w_kolejnosci_wyznaczonej_przez_p_wolaj
{
przechodz_komorki( x-1, y );
przechodz_komorki( x+1, y );
przechodz_komorki( x, y-1 );
przechodz_komorki( x, y+1 );
}
}
Takie podejście jednak nie sprawdzi się w przypadku dużych zaczynów z powodu ograniczenia pamięci stosu
dostępnego programom. W praktyce, w programie napisanym w C# nie byłem już w stanie uzyskać
labiryntu o rozmiarach 64x64, bowiem program kończył się oczywistym wyjątkiem "Stack overflow".
Problem ten rozwiązałem przez wersję iteracyjną tego algorytmu. Wymagało to zaimplementowania
stosu, na którym podczas przejścia do nowej komórki odkłada się aktualną pozycję oraz wskaźnik, który mówi
które kierunki drogi z danej komórki były już próbowane.
Na przykład jeśli algorytm znajduje się akurat
w komórce (4, 5) i przechodzi do komórki (4, 6) to na stos odkłada informację
(4, 5, stan_kierunków | kierunek_wschód).
Kiedy podczas analizy drogi algorytm dochodzi do komórki, dla której
wszystkie kierunki ruchu zostały już przeanalizowane, po prostu ściąga ze stosu stan obliczeń i próbuje
kolejnych, jeszcze nie wykorzystanych dróg dla tego stanu.
Decydowanie o usuwaniu ścian między komórkami podczas przechodzenia zaczynu
Drugą trudnością jest konieczność sprawdzenia w każdym kroku czy dwie komórki mają już jakieś połączenie.
Chodzi o to, aby każde dwie komórki były połączone dokładnie jedną drogą. Jeśli komórka źródłowa i docelowa
są już połączone jakąś drogą, to algorytm nie będzie próbował usuwać ściany pomiędzy nimi.
Tak naprawdę decydowanie o tym czy dwie komórki są już połączone czy nie wcale nie jest takie proste.
W naiwnym podejściu wymaga to ponownej analizy całego zbudowanego do tej pory labiryntu!
Wykorzystałem więc pewną wersję algorytmu przypisywanego Robertowi E. Tarjanowi (laureatowi m.in. nagrody
im.Turinga za badania nad podstawiami algorytmiki). Algorytm, w ujęciu takim w jakim przedstawiony był
w materiałach źródłowych, wydał mi się pomimo swojej prostoty i tak niepotrzebnie zawiły. Postanowiłem go
uprościć jeszcze bardziej.
Pomysł jest następujący: w dodatkowej tablicy (nazwanej tablicą baz)
będziemy przechowywali informację o tym, które komórki są
już połączone. Tablica indeksowana będzie indeksem komórki ( index(X, Y) = szerokosc_labiryntu * Y + X )
i przechowywać będzie informacje dwojakiego rodzaju:
- liczbę -1, która oznacza - ta komórka jest ogonem pewnego segmentu komórek połączonych
- liczbę nieujemną, która oznacza numer kolejnej komórki w segmencie
Połączmy na przykład komórki (0, 0), (0, 1) i (0, 2) w jeden łańcuch. Odpowiednie indeksy komórek:
index(0, 0)=0, index(0, 1)=1, index(0, 2)=2
Tablica baz wyglądać będzie tak:
[0] : -1
[1] : 0
[2] : 1
...
Aby obliczyć komórkę bazową danej komórki, obliczamy jej index a następnie przeszukujemy
tablicę baz tak długo, aż trafimy na ogon sekwencji (kod z programu TorqMaze 0.01):
int base_cell( int tIndex )
{
int index = tIndex;
while ( maze_base[ index ] >= 0 )
{
index = maze_base[ index ];
}
return index;
}
Sprawdzenie czy dwie komórki C1 i C2 są połączone jest proste - wystarczy obliczyć komórkę bazową dla
C1 i C2 i sprawdzić czy to jest ta sama komórka. Dzieje się tak dlatego, że dwa obszary rozłączne można
połączyć w jeden, przez przypisanie komórce bazowej jednego z obszarów wskaźnika na komórkę bazową drugiego:
void merge( int index1, int index2 )
{
// merge both lists
int base1 = base_cell( index1 );
int base2 = base_cell( index2 );
maze_base[ base2 ] = base1;
}
Na przykład dwa rozłączne obszary
[0] : -1
[1] : 0
[2] : 1
oraz
[3] : -1
[4] : 3
[5] : 4
są łączone przez funkcję merge() jako:
[0] : -1
[1] : 0
[2] : 1
[3] : 0
[4] : 3
[5] : 4
Zauważmy, że wartość komórki bazowej base_cell() dla wszystkich tych komórek wynosi 0, czyli rzeczywiście
wszystkie te 6 komórek znajduje się teraz w jednym obszarze.
Łącznenie przechodzenia przez zaczyn z usuwaniem ścian
Aby niepotrzebnie nie komplikować algorytmu, obie części (przechodzenie i usuwanie ścian) wykonywane są w jednym przebiegu. Dzięki temu po przejściu całego labiryntu algorytm usuwa tylko te ściany, które nie powodują
powstawiania cykli ( wielu dróg między tymi samymi punktami ). Informacja o ścianach zapisywana
jest w odpowiedniej strukturze, kolejne przejście przez nią pozwala na utworzenie bitmapy zawierającej odpowiedni
obraz.
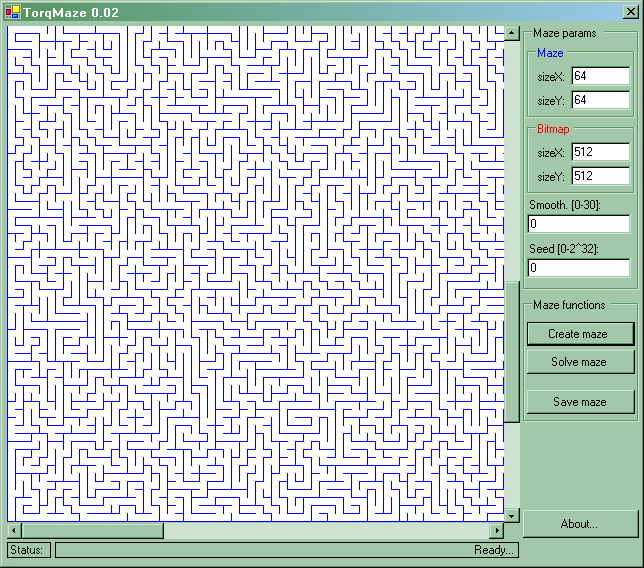
Wygląd interfejsu programu TorqMaze 0.02
Szukanie drogi
Okazuje się, że istnieją różne sprytne algorytmy szukania drogi w labiryntach.
Przedstawię najprostszy z nich, pewny i niezawodny, jednak wymagający sporych nakładów pamięciowych
(tablicy o rozmiarach takich jak labirynt oraz, dodatkowo, pomocniczej listy).
Algorytm działa bardzo prosto.
Pokażę go na przykładzie tego oto labirynciku:

W owej pomocniczej tablicy (nazwijmy ją mazePath) będziemy sukcesywnie budować obraz
drogi pomiędzy punktem początkowym i końcowym. Na początek wypełnijmy tę tablicę wartościami -1.
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
Algorytm rozpoczynamy wpisując w pole początkowe wartość 0.
| 0 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
Następnie wykonujemy i-ty krok algorytmu tak długo aż nie osiągniemy punktu końcowego:
- wszystkie pola labiryntu sąsiadujące z polami wypełnionymi
w poprzednim kroku (ale tylko te, które nie są jeszcze wypełnione)
wypełniamy wartościami i oczywiście pod warunkiem, że posuwamy się po
ścieżce labiryntu (nie wolno przechodzić przez ściany, to oczywiste)
Interpretacja takiego postępowania jest prosta - w i-tym
kroku oznaczamy pola osiągalne z pola wyjściowego w ... i krokach.
Najprościej będzie zobaczyć kolejne kroki algorytmu na naszym przykładzie:
| 0 | 1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| 0 | 1 | -1 | -1 |
| -1 | 2 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| -1 | -1 | -1 | -1 |
| 0 | 1 | -1 | -1 |
| 3 | 2 | 3 | -1 |
| -1 | 3 | -1 | -1 |
| -1 | -1 | -1 | -1 |
...aż 3 pola są osiągalne w 3 krokach...
...
| 0 | 1 | -1 | -1 |
| 3 | 2 | 3 | -1 |
| 4 | 3 | 8 | -1 |
| 5 | 6 | 7 | 8 |
...a w 8 kroku osiągamy cel!
W tym momencie pierwsza część algorytmu jest zakończona - w ósmym kroku osiągnięto pole końcowe.
Należy jedynie ustalić drogę. W tym celu posuwając się od pola końcowego, w kolejnych krokach
szukamy kolejno malejących wartości (u nas od 8 do 0) stanowiących drogę pomiędzy punktem końcowym
a początkowym.
W tym momencie droga jest gotowa.

Szczegóły implementacji (w której przecież chodzi o wydajność) są na tyle nieistotne, że je pominę -
odsyłam do kodu źródłowego TorqMaze 0.02. Jako ćwiczenie proponuję przetestować ten algorytm
na bardziej skomplikowanych labiryntach.




