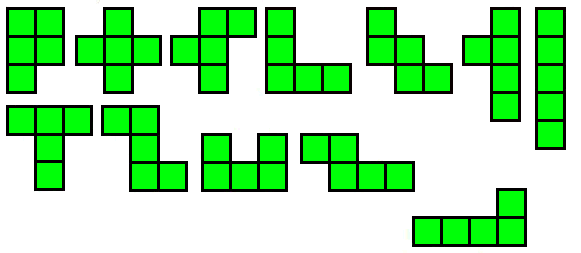
Zadania (na ćwiczenia i do domu):
I. KR 1.1-1.5
II. Jeśli x0 jest pewnym przybliżeniem pierwiastka równania f(x)=0 to lepszym przybliżeniem jest:
Zadania (na ćwiczenia i do domu):
I. KR 1.6-1.14
II. Zgadywanka: program losuje liczbę z przedziału [0-100], zadaniem użytkownika jest zaś odgadnięcie tej liczby.
Przykładowa sesja programu (komunikaty programu oznaczono "K", informacje użytkownika "U"):
K: Podaj liczbę z przedziału [0-100] U: 75 K: zbyt duża U: 56 K: zbyt duża U: 34 K: zbyt mała U: 48 K: zbyt duża U: 37 K: poprawnaLiczbę można ustalić jako stałą w programie lub skorzystać z funkcji rand() z biblioteki stdlib.
22.X
Zadania (na ćwiczenia i do domu):
I. KR 1.15, 1.19
II. Napisać program który dokonuje konwersji liczb między różnymi formatami. Program powinien poprawnie
obsługiwać formaty od binarnego do szesnastkowego (czyli o podstawach od 2 do 16). Dla formatów zapisu
używających więcej niż 10 cyfr przyjmujemy standardowy sposób zapisu liczb za pomocą dużych liter
alfabetu łacińskiego: A-F.
Wskazówka. Napisać funkcje o zadanych prototypach:
int KonwersjaXNa10(char* sLiczba, int iBaza), która będzie zamieniać napis (liczbę) zawarty w tablicy sLiczba z systemu o podstawie iBaza do systemu dziesiątkowego
void Konwersja10NaX(int iLiczba, int iBaza, char* xLiczba), która będzie zamieniać liczbę iLiczba z systemu dziesiątkowego do systemu o podstawie iBaza i wynik zapisze w tablicy xLiczba
Funkcji tych program mógłby użyć do przekształcenia liczby z systemu o podstawie X do systemu dziesiątkowego, a następnie do przekształcenia liczby z systemu dziesiątkowego do systemu o podstawie Y. Program powinien działać w pętli, w której użytkownik wprowadzałby dane wejściowe. Program powinien być dodatkowo odporny na przypadkowe błędy, np. wprowadzenie niepoprawnych symboli wejściowych. Oto zapis przykładowej sesji programu:
K: Baza systemu źródłowego [2-16, 0 - koniec] U: 8 K: Podaj liczbę w systemie o podstawie 8 U: 4554 K: Baza systemu docelowego U: 16 K: Wynik: 4554 [podstawa 8] = 96C [podstawa 16] K: Baza systemu źródłowego [2-16, 0 - koniec] U: 0 K: Koniec programu...
29.X
Rozwiązywanie zaległych zadań. Systemy pozycyjne.
Zadania:
I. KR 2.2, 2.4-2.8
5.XI
Rozwiązywanie zaległych zadań. Pliki nagłówkowe, podział programów na mniejsze części składowe.
Zadania:
I. KR 3.2, 3.3, 4.1-4.4
II. Obliczyć sumy szeregów 1/n2, 1/n3 dla n>=1
12.XI
Kololwium
19.XI
Rekurencja, preprocesor
Przykład prostej funkcji rekurencyjnej:
int silnia( int n )
{
if ( n==1 ) return 1;
else return n*silnia(n-1);
}
int iFib( int n )
{
if ( n<2 )
return n;
else
{
int i1 = 1, i2 = 1, sum;
for ( int i=2 ; i<n; i++ )
{
sum = i1+i2;
i1 = i2;
i2 = sum;
}
return i2;
}
}
int Fib( int n )
{
if ( n<2 ) return n;
else return Fib(n-2)+Fib(n-1);
}
int main(int argc, char *argv[])
{
printf("rek: %d\n", Fib(6) );
printf("itr: %d\n", iFib(6) );
}
Porównanie czasów wykonania (AMD K6-2 450Mhz):
| i | Fib(i) | Rekurencja (sek.) | Iteracja (sek.) |
| 30 | 832040 | 0.170 | 0.000 |
| 35 | 9227465 | 1.050 | 0.000 |
| 39 | 63245986 | 6.650 | 0.000 |
| ... | ... | rośnie bardzo szybko | 0.000 |
int szachownica[12][12];
int xk,yk,nr,rozwiazanie;
void przygotuj_pola()
{
int i,j;
for (i=0;i<12;i++)
for (j=0;j<12;j++)
szachownica[i][j]=1;
for (i=2;i<10;i++)
for (j=2;j<10;j++)
szachownica[i][j]=0;
}
void umiesc_konika(int x,int y,int numer)
{
int i,j,k,ch;
if (szachownica[x][y]==0)
{
szachownica[x][y]=numer;
if (numer==64)
{
printf("Rozwiazanie: %d\n",rozwiazanie);
rozwiazanie++;
for (i=2;i<10;i++)
{
for (j=2;j<10;j++)
{
printf("%3d ",szachownica[j][i]);
}
printf("\n");
}
}
umiesc_konika(x+1,y-2,numer+1);
umiesc_konika(x+2,y-1,numer+1);
umiesc_konika(x+2,y+1,numer+1);
umiesc_konika(x+1,y+2,numer+1);
umiesc_konika(x-1,y+2,numer+1);
umiesc_konika(x-2,y+1,numer+1);
umiesc_konika(x-2,y-1,numer+1);
umiesc_konika(x-1,y-2,numer+1);
szachownica[x][y]=0;
}
}
void main()
{
przygotuj_pola();
xk=2;yk=2;nr=1;rozwiazanie=1;
umiesc_konika(xk,yk,nr);
}
Zadania:
I. 4.12, 4.13, 4.14
II. Problem 8 hetmanów: na szachownicy o wymiarach 8x8 pól należy rozstawić 8 hetmanów tak, aby się nawzajem nie zbijały (rozwiązanie)
III. Napisz rekurencyjną funkcję obliczającą xn według wzoru xn = x * xn-1
IV. Napisz rekurencyjną funkcję obliczającą NWD(n, m) zwracającą największy wspólny dzielnik dwóch liczb całkowitych n i m na podstawie definicji:
NWD(n, m) = m, jeśli m<=n i n mod m = 0
NWD(n, m) = NWD(m, n), jeśli n<m
NWD(n, m) = NWD(m, n mod m), w przeciwnym razie
V. Napisz rekurencyjną funkcję obliczającą współczynniki dwumianowe Newtona ( "n po k" ) zgodnie z definicją:
Newton( n, k ) = 1, jeśli k=0 lub k=n
Newton( n, k ) = Newton( n-1, k-1 ) + Newton( n-1, k )
VI. Przeczytać z KR rozdział 5.
26.XI
Wskaźniki
Zadania:
I. KR 5.3-5.6, 5.8-5.10
II. (dla chętnych) Pentomino, to prosta logiczna łamigłówka. Do dyspozycji mamy 12 klocków, z których każdy składa się z 5 kostek.
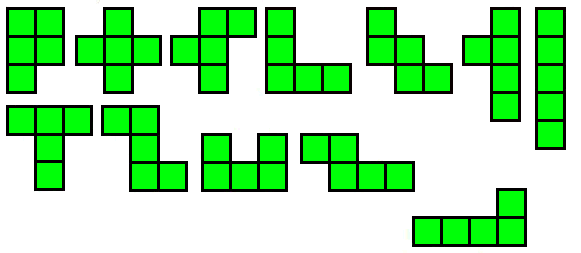

| Prostokąt | Rozwiązań |
| 10x6 | 2339 |
| 12x5 | 1010 |
| 15x4 | 368 |
Struktury
Przykładowa implementacja prostej kartoteki osobowej.
Zadania:
I. Dokończyć modyfikacje przykładowego programu wg. poleceń zawartych w kodzie programu
II. KR 5.14, 5.15
III. Przeczytać podrozdział 5.12. Przepisać i uruchomić oba programy dcl i undcl
10.XII
Parametry wywołania programu, zmienna długość listy argumentów, sortowanie.
Oto trzy przykładowe algorytmy sortujące:
Zadania:
I. Przeczytać cały rozdział 7 z KR
II. KR 7.1, 7.3, 7.6 (wypisywać numer pierwszego znaku, a nie wiersza)
III. Poczytać o innych algorytmach sortujących:
Literatura:
17.XII
Garść świątecznych programów. Rozwiązania zaległych zadań.
Zadania:
Bardziej precyzyjnie: dane są dwa pliki wejściowe q1.bin i q2.bin. Ich zawartość nie jest znana (może być binarna, mogą to być jakieś programy, teksty, pliki MP3, cokolwiek). Program powinien przeanalizować oba pliki i utworzyć nowy plik, q.pat, w którym zapisałby informację potrzebną do odtworzenia zawartości pliku q2.bin przy danej zawartości pliku q1.bin. Rozwiązanie tego zadania będzie więc składać się z dwóch programów:
Należy wymyślić sposób analizy danych wejściowych oraz algorytm tworzenia danych "łatek". Na zajęciach porównamy gotowe rozwiązania według zadanego kryterium (czyli rozmiaru plików łatek).
Nasz program mógłby znaleźć zastosowanie w następującej sytuacji: wyobraźmy sobie że użytkownik dysponuje wersją 1.0 naszego programu, nazwijmy go P. Obraz programu P składa się z wielu plików, w tym z pliku q1.bin. W wersji 1.1 naszego programu plik q1.bin uległ niewielkiej zmianie w stosunku do wersji 1.0. Może się jednak okazać, że plik q1.bin ma powiedzmy 100MB. Przesłanie użytkownikowi 100MB pliku q1.bin w nowej wersji nie jest możliwe. Możliwe byłoby jednak wysłanie użytkownikowi naszego programu do odtwarzania łatki wraz z wcześniej przygotowaną (programem do tworzenia łatki) łatką q.pat, która powiedzmy że zajmowałaby 100kB. Użytkownik mógłby uruchomić program do odtwarzania łatki, który z pliku q1.bin w wersji 1.0 odtworzy przy pomocy łatki plik q1.bin w wersji 1.1.
Literatura:
[1] Lech Pijanowski, Przewodnik gier, wyd.ORENDA, Warszawa 1997