8.X
Przykłady prostych programów Windowsowych. Zapoznanie ze strukturą GDI. Funkcje graficzne GDI.
Zadanie domowe nr.1:
Należy, korzystając z funkcji GDI, napisać program, który na powierzchni okna maluje wykres funkcji x^2 i sin(x), jednak wykresy są poprawnie skalowane do wymiarów okna podczas zmieniania rozmiarów okna. Wykresy powinny być malowane różnymi kolorami (zapoznać się z funkcjami CreatePen(), SelectObject(), DeleteObject() ).
Linki:
15.XKomunikaty systemowe:
Należy, korzystając z funkcji GDI, napisać program, który pozwala rysować na powierzchni okienka dowolne kształty. Rysowanie odbywa się przez przytrzymanie lewego przycisku myszy i poruszanie myszą po powierzchni okna. Naciskanie klawiszy 'p' 'e' 'b' itp. powinno przełączać program w tryb rysowania figur, np. po naciśnięciu 'p' i dwukrotnym kliknięciu na powierzchni okna, program powinien narysować prostokąt o zadanych rogach - w ten sposób obsłużyć kilka funkcji graficznych (3-4).
22.XInicjalizacja i korzystanie z OpenGL przez bibliotekę GLUT oraz przez Wiggle.
Przykład 22.X.1
Przykład 22.X.2
Podczas zajęć należy:
Należy napisać program, który rysuje na ekranie
trójkąt o dowolnie zadanych wierzchołkach (przez wskazanie myszą, wprowadzenie z konsoli etc). Pseudokod takiej procedury można znaleźć tutaj.
Rozwiązanie zadania powinno polegać na wykorzystaniu gotowej funkcji w 3 wersjach programu:
Funkcje glBegin() i glEnd().
Przykład 29.X.1
Przykład 29.X.2
Podczas zajęć należy:
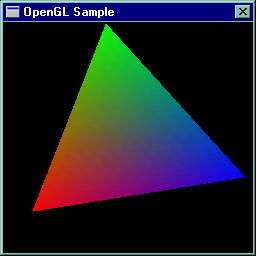
Należy funkcję z zadania 3 rozbudować o kolorowanie powierzchni trójkąta. Bardziej formalnie: parametrami wejściowymi funkcji Trojkat() powinny być nie tylko tablice x[3] i y[3] określające współrzędne wierzchołków, ale dodatkowo tablice r[3], g[3] i b[3] określające składowe kolorów w wierzchołkach.

Skoro wartość współrzędnej x może być tak wyliczana, to na pewno da się tak samo wyliczać wartości składowych kolorów R G i B. To oznacza, że interpolowane wdłuż krawędzi będą aż 4 wartości: x, r, g i b.
Modyfikacji musi ulec także funkcja LiniaPozioma(). W rozbudowanej wersji będzie ona otrzymywała jako parametry także r, g i b początkowego i końcowego punktu. Znając długość lini [abs(x2-x1)] można łatwo wyliczyć nowe przyrosty dr', dg' i db', które posłużą do wyliczenia wartości r, g i b kolejnych punktów lini poziomej.
Program będący rozwiązaniem zadania powinien korzystać z OpenGL.
5.XIMacierze widoku obiektów, macierze rzutowe. Funkcje: glOrtho(), gluPerspective(), glTranslate(), glRotate(), glScale(). Pozycja obserwatora w scenie. Funkcja glLookAt().
Przykładowy program: Przykład.5.XI.I.
Zadanie domowe nr.5:
Należy zaprojektować prostą scenę trójwymiarową złożoną z kilku obiektów. Podstawą całej sceny powinna być dość spora płaszczyzna ('podłoga'), na niej zaś rozmieszczone powinny być co najmniej 5 obiektów (torusy, sześciany, kule, stożki itp.). Niektóre obiekty koniecznie powinny być ruchome, tzn. np. sześcian czy torus może obracać się dookoła osi symetrii.
Program powinien być interaktywny, to znaczy użytkownik za pomocą klawiatury lub myszy powinien mieć możliwość poruszania się równolegle do płaszczyzny będącej 'podłogą' całej sceny. Całość powinna być wizualizowana w rzucie perspektywicznym.
Program będzie przyjęty jeśli:
Uwaga! Przemieszczanie obserwatora po świecie 3D jest trywialne obliczeniowo przy ruchu do przodu/do tyłu. Znacznie trudniej jest pozwolić obserwatorowi na swobodny obrót w lewo/w prawo. Wymaga to bowiem zastosowania wzoru na obrót punktu (tu: punktu na który patrzy obserwator) wokół dowolnej osi (tu: osi wyznaczonej przez kierunek góra/dół obserwatora). Odpowiedni wzór nosi nazwę wzoru Rodriguesa (Rodrigues formula) i wygląda następująco (przy założeniu, że kierunek obrotu zaczepiony jest w początku układu współrzędnych):
Oświetlenie. Źródło światła.
Obiekty w OpenGL są oświetlane przy pomocy trzech rodzajów oświetlenia:
Światło to nie wszystko. Każdy obiekt wykonany jest z jakiegoś materiału, który ma swój własny kolor i dzięki temu inaczej odbija światła różnych kolorów. Co więcej właściwością materiału, z którego zbudowany jest obiekt, może być odbijanie światła odbłysków, zaś pochłanianie światła otaczającego i rozproszonego (np. powierzchnie metaliczne) lub zupełnie odwrotnie - odbijanie światła otaczającego i rozproszonego a pochłanianie światła odbłysków (np. powierzchnia kredy).
Podsumowanie funkcji OpenGL dot. operowania światłem:
glEnable(GL_LIGHTING) informuje OpenGL, że należy przeliczać również oświetlenie obiektów
glBegin(GL_TRANGLES)
glNormal3f(0.0, -1.0, 0.0);
glVertex3f(0.0, 1.0, 0.0);
glVertex3f(1.0, 1.0, 0.0);
glVertex3f(0.0, 1.0, 1.0);
glEnd(); przykład określania wektora normalnego do powierzchni
glEnable(GL_NORMALIZE); informuje OpenGL, że ma sam normalizować wektory normalne do powierzchni
Uwaga. Obiekty rysowane automatycznie za pomocą funkcji GLUT (np. glutSolidTeapot()) mają już przypisane wektory normalne do powierzchni.
glEnable(GL_COLOR_MATERIAL); informuje OpenGL, że właściwości materiału z jakiego zbudowany jest obiekt mają wynikać z koloru obiektu (do oświetlania obiektów OpenGL używa informacji o materiałach z jakich są zbudowane).
GLfloat ambientLight[] = { 0.1, 0.1, 0.1, 1.0};
GLfloat specref[]={1.0f, 1.0f, 1.0f, 1.0f};
glLightv(GL_LIGHT0, GL_AMBIENT, ambientLight);
glEnable(GL_LIGHT0); przykład ustawienia światła otaczającego
glMaterialfv(GL_FRONT, GL_SPECULAR, specref); ustawia właściwości odbłysków materiału glMateriali(GL_FRONT, GL_SHININESS, 128); określa stopień połyskliwości mateirału
glLightfv(GL_LIGHT0, GL_POSITION, lightPos); pozycja źródła światła
glLightfv(GL_LIGHT0,GL_SPOT_DIRECTION,spotDir); kierunek źródła światła
glLightf(GL_LIGHT0, GL_SPOT_CUTOFF, 60.0f); kąt rozwarcia światła
glLightf(GL_LIGHT0, GL_SPOT_EXPONENT, 100.0f); jasność źródła światła
Uwaga. Maksymalna ilość źródeł światła na jaką pozwala OpenGL określona jest za pomocą stałej GL_MAX_LIGHTS.
Konkretny przykład zastosowania funkcji: Przykład.12.XI.I.
W trakcie zajęć należy:
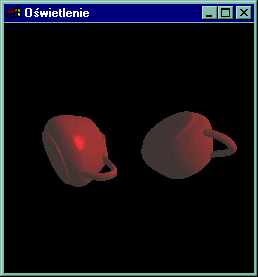
Należy scenę zaprojektowaną w zadaniu nr.5 wzbogacić o 3 źródła światła: światło czerwone, światło zielone i światło niebieskie. Wymagania programu:
Wskazówki:
19.XI
glPushAttrib(GL_LIGHTING_BIT);
glDisable(GL_LIGHTING);
...rysuj jakieś obiekty które nie będą oświetlane...
glPopAttrib();
GLfloat specref[2][4]= { {1.0f, 1.0f, 1.0f, 1.0f}, {0.0f, 0.0f, 0.0f, 0.0f}};
glMaterialfv(GL_FRONT, GL_SPECULAR, specref[0]); - najwyższy stopień połyskliwości
glMaterialfv(GL_FRONT, GL_SPECULAR, specref[1]); - brak połyskliwości
Zmian takich można oczywiście dokonywać w trakcie rysowania obiektów.
Cienie, tekstury
Najprostszy sposób rysowania cieni w OpenGL polega na rysowaniu dodatkowo kopii zadanego obiektu, modyfikując wcześniej macierz widoku tak, aby obraz obiektu trafiał w postaci spłaszczonej na płaszczyznę na której ma powstać cień. Tak naprawdę bowiem cień jest obrazem jaki można by uzyskać, gdyby obserwować obiekt z punktu w którym znajduje się światło.
W przykładowym programie czajnik najpierw rysowany jest tak jak zwykle, a następnie macierz jego widoku jest modyfikowana tak, aby uzyskać jego rzut na płaszczyznę, na którą ma padać cień. Ten drugi czajnik rysowany jest kolorem czarnym. Proszę zwrócić uwagę na pewną sztuczkę: "podłoga" jest płaszczyzną o współrzędnej y = -150.0. Cień czajnika rzutujemy na płaszczyznę o y = -149.0. Unikamy dzięki temu pewnego dość przykrego zjawiska (jakiego? jak je wytłumaczyć?).
Kod źródłowy przykładowego programu demonstrującego tę technikę: Przykład.19.XI.I.

glEnable(GL_TEXTURE_2D);
oraz ustawić zawartość tekstury w pamięci OpenGL:
glTexImage2D(...);
Aby za każdym razem nie wołać tej funkcji wprost w kodzie do przełączania tekstur, skorzystamy z tzw. list wyświetlania.
Ogólnie listy wyświetlania służą do przyspieszania rysowania. Dowolny ciąg poleceń rysowania wstawiamy między wywołania:
glNewList( idList, GL_COMPILE. );
...
glEndList();
a następnie wołamy przez:
glCallList(idList);
Efektem działania list wyświetlania jest znaczne przyspieszenie tworzenia obrazu przez OpenGL.
Parametry nakładania tekstury można modyfikować za pomocą funkcji:
glTexEnvi( ... );
glTexParametri( ... );
Na przykład odwzorowywanie tekstur z liniową interpolacją włączamy przez:
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);
glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
Kod źródłowy programu: Przykład.19.XI.II.
W trakcie zajęć należy
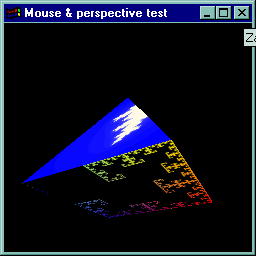
Należy scenę zaprojektowaną w zadaniu 5 (i rozbudowaną w zadaniu 6) wzbogacić o obsługę cieni i mapowania tekstur. Wymagania programu:
26.XI
Przezroczystość
OpenGL pozwala łatwo korzystać z przezroczystości. W określaniu wzajemnej relacji kolejno rysowanych prymitywów można wykorzystać informacje z dodatkowego kanału określającego przezroczystość obiektów (tzw. kanał alpha), można też po prostu wykorzystać informacje o kolorach obiektów. Metoda ma tylko jeden mankament - obiekty uzyskują przezroczystość względem siebie w takiej kolejności w jakiej trafiają do bufora obrazu.
W przykładowym programie można ten efekt zaobserwować bardzo dokładnie - przy obracaniu obiektu zauważamy, że ściany są względem siebie przezroczyste tylko w takiej kolejności w jakiej są rysowane: ściana 1 nie jest przezroczysta, ściana 2 'przepuszcza' obraz ściany 1, ściana 3 - 2 i 1 itd.
W praktyce te ściany obiektów które mają być przezroczyste należy więc rysować na samym końcu.
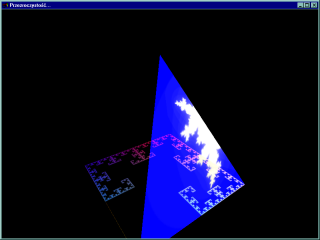
Kod źródłowy programu: Przykład.26.XI.II.
Zadanie domowe nr.8:
Zaimplementować algorytm Bresenhama rysowania linii i okręgu. Narysowany okrąg należy wypełnić jednolitym kolorem. Do tego celu należy zaimplementować jakiś algorytm wypełniania konturów.
3.XIIFormaty plików z obiektami 3D
Oczywiście w rozbudowanym programie z interaktywną grafiką trójwymiarową obiekty nie powinny być "zaszyte w kodzie". O wiele wygodniej jest wydzielić opis obiektu do osobnej struktury.
Zadanie na zajęcia: przygotowano zestaw przykładowych plików zapisanych w trywialnym formacie. Należy "rozgryźć" (cudzysłowy sugerują że tak naprawdę nie ma tam czego rozgryzać) strukturę formatu pliku oraz napisać program, który potrafi wczytać opis obiektu z pliku i pokazać obiekt w środowisku 3D.
Zadanie domowe nr.9.
Zapoznać się z jakimś popularnym formatem opisu scen trójwymiarowych (do wyboru: *.3DS, *.ASC, *.OBJ, *.X, inne?), wykorzystywanym w jakimś znanym narzędziu do modelowania 3D (3D Studio, Wavefront, Lightwave itp.). Własnoręcznie przygotować (lub w przypadku braku dostępu do w/w narzędzi - ściągnąć z sieci) proste obiekty w wybranym przez siebie formacie i rozszerzyć swoją scenę 3D o wyświetlanie tych obiektów.
Wskazówki:
Zaawansowana technika generowania cieni przy użyciu bufora szablonów
Programista tworzący program przy użyciu OpenGl ma do dyspozycji kilka specjalizowanych buforów. Kilka z nich (bufory głębokości, koloru) są nam już znane. Bardzo przydatny okazuje się również tzw. bufor szablonów, który służy do maskowania rysowania fragmentów sceny.
Typowym zastosowaniem buforów jest zamaskowanie obszaru obrazu na którym rysowany jest na przykład panel sterowania jakiegoś pojazdu, bądź konsola sterowania widokiem. Okazuje się, że bufor szablonów można bardzo sprytnie wykorzystać do generowania realistycznych cieni.
Przykłady.10.XII.I i II. Autorami programów są Jeff Molofee i Tom McReynolds.
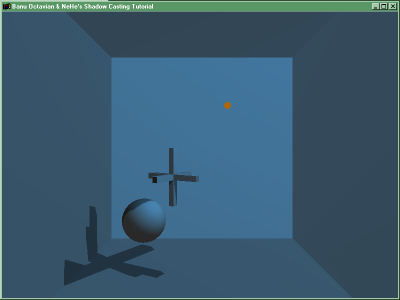
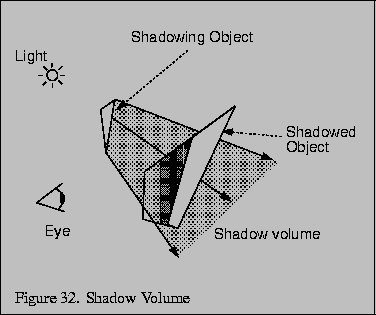
Krawędzie brył tworzących wolumeny cieni powstają z promieni wysyłanych przez źródło światła. Przechodząc przez wierzchołki obiektu ocieniającego (tego który rzuca cień) i kontytuując swój bieg przez scenę 3D, te promienie wysyłane od źródła światła tworzą nieskończone "pseudo-piramidy". W modelu obliczeniowym można wyeliminować nieskończoność takiego wolumenu cienia przez ograniczenie go tak, aby obejmował najdalsze obiekty w scenie 3D. W ten sposób otrzymujemy wielobok w przestrzeni 3D tworzący wolumen cienia danej ściany. Jego wnętrze zawiera te części sceny 3D, które leżą w cieniu odpowiadającej mu ściany. Ściślej - wolumen cienia dla każdej ściany tworzy ścięty ostrosłup, którego górną ścianę tworzy ściana rzucająca cień, jego ściany tworzą granice cienia, zaś podstawa takiego ostrosłupa ogranicza go na tyle daleko, aby taki wolumen nie był "zbyt krótki", tzn. aby obejmował najdalsze obiekty, które mogłyby leżeć w jego wnętrzu.
Bufor szablonów jest wykorzystywany do określenia które fragmenty sceny leżą w cieniu. Podczas rysowania wolumenu cienia, odpowiednie wartości w buforze szablonu są najpierw inkrementowane przy rysowaniu ścian wolumenu zwróconych przodem do obserwatora, a następnie dekrementowane przy rysowaniu ścian wolumenu zwróconych tyłem do obserwatora. Ponieważ rysowanie w buforze szblonu ustawione jest tak, aby wykorzystywać informację zawartą w buforze głębokości, to w rezultacie te punkty sceny które leżą w cieniu będą miały niezerową wartość w buforze szablonu.
Oto podsumowanie algorytmu tworzenia cieni dla jednego źródła światła:
Poprawne zaimplementowanie tej techniki wymaga dodatkowych struktur danych oraz dodatkowych, niestandardowych obliczeń. Dlatego należy bardzo uważnie przestudiować kod przykładowego programu.
Problemy programistyczne dla chętnych:
Zadanie domowe nr.10.
Jeszcze jednym buforem, którego do tej pory nie znamy jest bufor akumulacji.
Dotrzeć do dokumentacji bufora akumulacji i zademonstrować jego działanie w dwóch przykładowych programach:
Programy powinny demostrować odpowiednie efekty na prostych bryłach bądź figurach płaskich.
DirectX jako alternatywa dla OpenGL
W trakcie zajęć należy poszukać na sieci jakichś tutoriali DirectX i zapoznać się z podstawami interfejsu tej biblioteki. W szczególności nauczyć się jak:
Zadanie domowe nr.11.
Zajęcia przeznaczone na realizację projektów.
Uwaga. Jest już DirectX 9.0 z dodatkowymi bibliotekami do C# (ukazał się 20 grudnia). Binaria oraz SDK (230MB) do pobrania ze strony Microsoftu. Kod programów DirectXowych napisanych w C# jest rzeczywiście bardzo czytelny, sama obsługa biblioteki jest bez porównania łatwiejsza niż w C++ (łatwość korzystania z DirectX w C# porównałbym do łatwości korzystania z GLUT w C).
Realizacja projektu jest obowiązkowa!.
Projekty mogą być realizowane samodzielnie, mogą być także realizowane w zespołach 2-osobowych, jednak wtedy podział obowiązków musi być ściśle sprecyzowany (to znaczy musi być wiadomo kto czym się zajmuje). Do końca grudnia należy przedstawić opis projektu (w postaci dokumentu papierowego), który musi zostać zaakceptowany przez prowadzącego. Składniki opisu projektu:
Propozycje projektów (inne spoza listy - po konsultacji z prowadzącym, można wykazać się pomysłowością).